7.2 Initialisation of the k-epsilon model
Initial values and boundary conditions must be
specified for 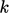 and
and 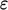 to solve their respective transport equations. The
ideal specification of boundary conditions for
to solve their respective transport equations. The
ideal specification of boundary conditions for 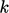 and
and 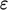 follows those for
follows those for
 described in Sec. 4.3
.
described in Sec. 4.3
.
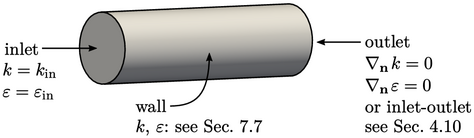
Turbulence fields require: a fixed value condition at inlets; zero gradient or inlet-outlet at outlets; and, a more complex specification at solid walls, introduced in Sec. 7.7 .
Inlet values  and
and 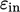 must therefore
be specified. There may be industry standards, published
recommendations or measured data to help select these values for
the specific problem being simulated.
must therefore
be specified. There may be industry standards, published
recommendations or measured data to help select these values for
the specific problem being simulated.
But more often than not, 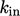 and
and 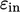 must be
estimated. Inlet and initial estimates of
must be
estimated. Inlet and initial estimates of 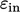 are usually based
on a Prandtl mixing length
are usually based
on a Prandtl mixing length 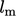 from the expression
from the expression
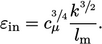 |
(7.4) |
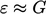 which can be
combined with the mixing length Eq. (6.21
) to give
which can be
combined with the mixing length Eq. (6.21
) to give
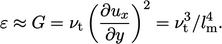 |
(7.5) |
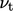 from Eq. (6.31
) yields Eq. (7.4).
from Eq. (6.31
) yields Eq. (7.4).
A value for 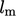 must then be specified
in order to calculate inlet and initial values of
must then be specified
in order to calculate inlet and initial values of 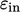 from
Eq. (7.4
). Procedures to estimate
from
Eq. (7.4
). Procedures to estimate
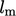 are described in Sec. 7.3
.
are described in Sec. 7.3
.
Inlet and initial estimates for 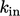 can be calculated
by
can be calculated
by
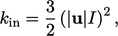 |
(7.6) |
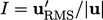 , the ratio of the
root-mean-square (RMS) of turbulent fluctuations
, the ratio of the
root-mean-square (RMS) of turbulent fluctuations 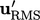 to the mean flow
speed
to the mean flow
speed 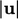 . The expression is derived from the definition
. The expression is derived from the definition 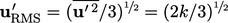 .
.
A value for 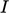 must then be specified
in order to calculate the inlet and initial values of
must then be specified
in order to calculate the inlet and initial values of 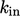 from
Eq. (7.6
). Procedures to estimate
from
Eq. (7.6
). Procedures to estimate
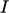 are also described in Sec. 7.3
. The values of
are also described in Sec. 7.3
. The values of
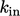 and
and 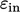 at inlet boundaries influence the solution throughout the
CFD simulation, so should be estimated as accurately as possible.
at inlet boundaries influence the solution throughout the
CFD simulation, so should be estimated as accurately as possible.
The accuracy of the initial (internal) values is not so critical, since they do not influence the solution beyond a short period at the beginning of a simulation.
Initial values can, however, affect stability during the early steps of a
CFD simulation. The flow boundary
conditions generally cause sudden impulses which can generate large
forces, causing fluctuations in the solution of 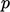 . Higher
. Higher 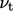 , based on
initial
, based on
initial 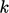 and
and 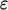 values, tends to cause larger fluctuations, which may make
the solution of the
values, tends to cause larger fluctuations, which may make
the solution of the 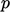 -equation unstable.
-equation unstable.

