7.7 Turbulence near walls
The characteristic velocity distribution in
turbulent boundary layers in Sec. 7.4
, provided wall
functions expressed as boundary conditions for 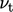 in Sec. 7.5
and Sec. 7.6
. Boundary
conditions also need to be specified for turbulence fields at solid
walls.
in Sec. 7.5
and Sec. 7.6
. Boundary
conditions also need to be specified for turbulence fields at solid
walls.
The turbulence generation 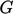 influences the
distribution of turbulence fields near a wall. At the wall,
influences the
distribution of turbulence fields near a wall. At the wall,
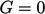 .
In the inertial sub-layer,
.
In the inertial sub-layer,  from Eq. (7.5
) with:
from Eq. (7.5
) with: 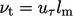 , obtained by combining
Eq. (6.21
) and Eq. (7.15
); and,
Eq. (6.24
).
, obtained by combining
Eq. (6.21
) and Eq. (7.15
); and,
Eq. (6.24
).
Since  decreases with increasing
decreases with increasing 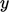 in the inertial
sub-layer,
in the inertial
sub-layer, 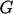 passes through a peak within the buffer layer (at
passes through a peak within the buffer layer (at
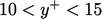 ).
).
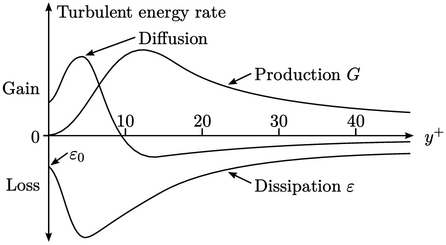
The peak in  causes a similar peak
in
causes a similar peak
in 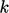 , shown in the following diagram. To the left of the peak,
turbulent energy is transported back towards the wall by diffusion
, shown in the following diagram. To the left of the peak,
turbulent energy is transported back towards the wall by diffusion
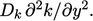 The profile of dissipation
The profile of dissipation 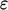 results from
results from 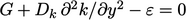 , obtained
from Eq. (7.1
). Very close to the wall
(
, obtained
from Eq. (7.1
). Very close to the wall
(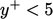 ),
diffusion is predominately molecular, such that it non-zero at the
wall. The dissipation
),
diffusion is predominately molecular, such that it non-zero at the
wall. The dissipation 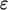 also has a non-zero value
also has a non-zero value 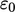 at the wall.
at the wall.
Wall functions and turbulence fields
When using a turbulence model, such as the
 model described in Sec. 7.1
, boundary conditions must be
specified for
model described in Sec. 7.1
, boundary conditions must be
specified for 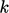 and
and 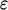 at solid walls. The distribution of
at solid walls. The distribution of 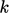 ,
non-dimensionalised as
,
non-dimensionalised as 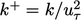 , close to the wall is shown below.
, close to the wall is shown below.

At the wall,  but it rises quickly
to a peak at
but it rises quickly
to a peak at 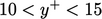 before levelling off at
before levelling off at 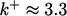 as
as 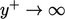 .
.
With wall functions, the height of the centre of
each near-wall cell should correspond to 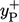 within the range
within the range
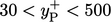 .
Viewed at that scale, the
.
Viewed at that scale, the 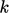 profile appears flat. For
profile appears flat. For 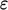 , there is no such
simple profile shape. These observations lead to the boundary
conditions for
, there is no such
simple profile shape. These observations lead to the boundary
conditions for 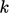 and
and 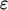 when using wall functions:
when using wall functions:
- zero
gradient for
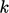 ;
; - calculated
near-wall cell value for
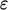 , according to:
, according to:
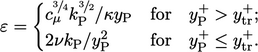 |
(7.26) |
 from the near-wall cell. The expression for
from the near-wall cell. The expression for
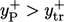 is
Eq. (7.4
) with Eq. (6.24
). The expression for
is
Eq. (7.4
) with Eq. (6.24
). The expression for
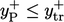 uses the asymptotic condition
uses the asymptotic condition  for
for 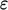 in Eq. (7.28
).
in Eq. (7.28
).

