7.10 Specific dissipation rate
The 
model is one of a family of two-equation models for turbulence.
With two equations, the models can represent each of the scales,
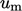and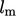 
, which characterise 
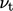. Most often,
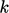is
used to represent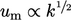 
.
The other variable must represent 
and so far we have
used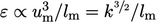 
with SI units 
. The specific dissipation rate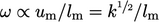 
, with SI units
of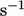 
, is a popular alternative for this variable in turbulence
modelling.
While Kolmogorov first proposed a two-equation
model,15
the 
models used in CFD originate from Wilcox.16
Here, “models” is plural since there are several versions of
model with modifications and additions from its original form.
The original 
model is
presented below (with some changes to the original variable names),
assuming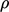 
= constant for direct comparison with
in
Sec. 7.1
.
 |
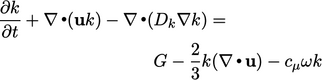(7.36) |
 |
(7.37) |
The standard model coefficients are
 |
(7.38) |
. Substituting in Eq. (6.31
) leads to a simple relation
for turbulent viscosity, given by
 |
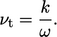(7.39) |
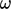can be calculated by
 |
(7.40) |
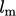, in a manner similar to 
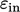in
Eq. (7.4
).
With wall functions, the boundary condition applied to
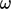set a near-wall cell value
according to
 |
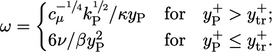(7.41) |
(
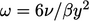) is a solution to the following equation for
the viscous sub-layer where diffusion and dissipation terms dominate
in Eq. (7.37
):
 |
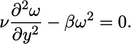(7.42) |
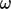in Eq. (7.37) and
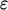in
Eq. (7.2
) are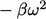 
and 
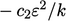respectively. The former is more stable in a numerical solution
since it is insensitive to variations in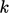 
.
