7.14 Thermal wall functions
Wall functions were introduced in
Sec. 7.5
in order to improve the
calculation of wall shear stress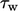 
when cells are too
large near a wall to resolve 
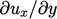accurately. The same
problem exists with heat flux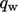 
and an under-predicted
.
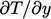As before, the universal character of the boundary layer can be
exploited, this time to improve the calculation of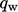 
.
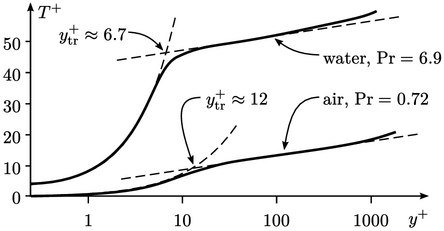
The temperature distribution is characterised
by Eq. (7.51
) for the viscous sub-layer,
and the log law Eq. (7.52
) for the inertial sub-layer.
The transition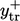 
for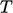 
occurs at the intersection of the two
equations, i.e. when
 |
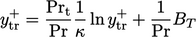(7.57) |
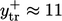by
Eq. (7.18
) for the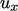 
profile, the
(iterative) solution of Eq. (7.57
) is dependent on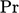 
and 
.
Using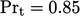 
and Eq. (7.55
) for 
, 
for air at
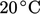with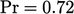 
. For water under the same conditions, 
and the corresponding
.
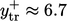A wall function can be derived which adjusts the
turbulent conductivity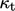 
, in a similar manner to 
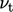in the standard
wall function in Sec. 7.5
. The model calculates
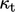for each patch face based on the near-wall cell 
.
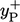No adjustment is made to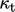 
when 
corresponds to the
viscous sub-layer. When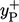 
corresponds to the inertial sub-layer,
is
calculated as
 |
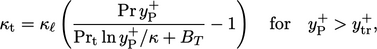(7.58) |
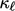denotes the laminar thermal conductivity, i.e. 
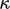from
Eq. (2.54
), to distinguish it from
Kármán’s constant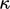 
. Eq. (7.58
) uses 
from
Eq. (7.19
), as in the standard
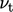wall function.
The wall function is derived based on adjusting
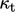to
improve the numerical calculation of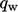 
by
 |
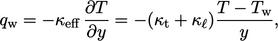(7.59) |
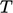represents a value close to the wall, e.g. in a near-wall cell. By
comparison, Eq. (7.49
) and Eq. (7.50
) combine to give
 |
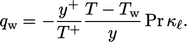(7.60) |
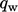is consistent between Eq. (7.59
) and
Eq. (7.60
) when
 |
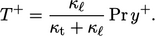(7.61) |
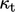according to
Eq. (7.58
).
