7.6 Alternative wall functions
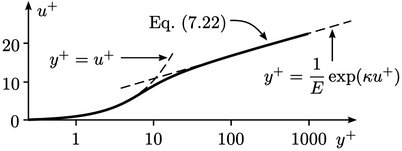
The standard wall function described in
Sec. 7.5
uses a function for
 that is discontinuous at
that is discontinuous at 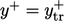 , switching to
, switching to  for
for 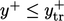 . A continuous wall function is available which evaluates
. A continuous wall function is available which evaluates 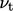 as
as  from a single
equation describing the universal character of the velocity profile
at high
from a single
equation describing the universal character of the velocity profile
at high 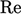 ,9
,9
 |
(7.22) |
 . The equation combines Eq. (7.11
) and Eq. (7.13
), “disabling”
Eq. (7.13
) at low
. The equation combines Eq. (7.11
) and Eq. (7.13
), “disabling”
Eq. (7.13
) at low 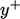 by subtracting low
order terms from a polynomial expansion of
by subtracting low
order terms from a polynomial expansion of 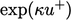 .
.
The wall function is applied by solving
Eq. (7.22
) for 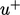 from
from 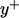 calculated from
Eq. (7.9)
using the near-wall cell centre height
calculated from
Eq. (7.9)
using the near-wall cell centre height 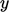 . The friction velocity
is calculated by
. The friction velocity
is calculated by  , where
, where 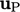 is the near-wall cell velocity. Finally,
is the near-wall cell velocity. Finally,
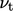 on
the wall patch is calculated from a numerical interpretation of
Eq. (7.20
),
on
the wall patch is calculated from a numerical interpretation of
Eq. (7.20
),
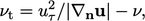 |
(7.23) |
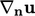 is the surface-normal velocity gradient. An iterative
method is required to invert Eq. (7.22) and
to accommodate other nonlinearities, e.g.
is the surface-normal velocity gradient. An iterative
method is required to invert Eq. (7.22) and
to accommodate other nonlinearities, e.g. 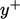 is itself a function
of
is itself a function
of  .
.
Rough wall function
The standard wall function in
Sec. 7.5
is applicable to smooth
walls so does not account for surface roughness. Roughness is significant when the
roughness “scale”  10 becomes larger than the thickness of the
viscous sub-layer.
10 becomes larger than the thickness of the
viscous sub-layer.
At higher surface roughness, turbulent eddies are
generated near the wall at a scale 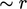 , rather than
, rather than
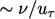 .
The viscous effects become negligible, causing the
non-dimensionalised distance to become
.
The viscous effects become negligible, causing the
non-dimensionalised distance to become 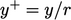 in the log law
Eq. (7.13
). To reflect this,
Eq. (7.13
) is modified to a form
in the log law
Eq. (7.13
). To reflect this,
Eq. (7.13
) is modified to a form
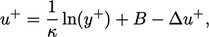 |
(7.24) |
 a roughness function, dependent on
a roughness function, dependent on 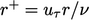 . An intuitive model
for
. An intuitive model
for 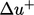 is11
is11
 |
(7.25) |
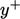 definition of Eq. (7.9
) at
definition of Eq. (7.9
) at  . As
. As 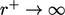 , it reduces to
Eq. (7.13
) using
, it reduces to
Eq. (7.13
) using 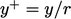 .
.
It is open to interpretation how to determine
 from roughness measurements of a surface. The parameter is
sometimes split into
from roughness measurements of a surface. The parameter is
sometimes split into 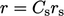 , where
, where 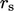 is a measured sand grain roughness height and
is a measured sand grain roughness height and
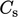 is
a coefficient that depends on the shape, consistency and packing of
the roughness elements. Using that approach, values of
is
a coefficient that depends on the shape, consistency and packing of
the roughness elements. Using that approach, values of 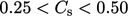 often yield a
good match between Eq. (7.24
) and measured data.
often yield a
good match between Eq. (7.24
) and measured data.
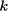 ’ is often used to
denote roughness, but we use ‘
’ is often used to
denote roughness, but we use ‘ ’ to avoid confusion with turbulent kinetic
energy.
’ to avoid confusion with turbulent kinetic
energy.
