7.11 Enhancements to the k-omega model
A comparison of the  and
and  models shows the
dissipation term is
models shows the
dissipation term is 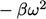 in Eq. (7.37
) for
in Eq. (7.37
) for  and
and 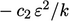 in
Eq. (7.2
) for
in
Eq. (7.2
) for 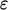 . While the
. While the 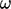 term behaves
well, the
term behaves
well, the 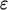 term is troublesome at a wall as
term is troublesome at a wall as  , so requires damping
in the low-
, so requires damping
in the low-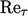 formulation in Sec. 7.9
to resolve the viscous
sub-layer.
formulation in Sec. 7.9
to resolve the viscous
sub-layer.
Its better dissipation term gives the
 model an advantage over
model an advantage over  in the near-wall region. The disadvantage
the original
in the near-wall region. The disadvantage
the original  model is its sensitivity to the freestream values of
model is its sensitivity to the freestream values of
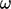 ,
which is not present in
,
which is not present in 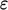 in the
in the  model. Neither model,
in their original form, performs well under adverse pressure
gradients.
model. Neither model,
in their original form, performs well under adverse pressure
gradients.
However, since its initial publication, many
enhancements have been made to the original  model, in particular
to address the problems mentioned above.
model, in particular
to address the problems mentioned above.
Cross-diffusion
The dependency on freestream values of
 is
addressed by the inclusion of a cross-diffusion term
is
addressed by the inclusion of a cross-diffusion term 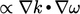 in the
in the
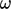 equation.17
The term is derived when the
equation.17
The term is derived when the 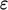 equation, e.g. Eq. (7.2
), is expressed in terms of
equation, e.g. Eq. (7.2
), is expressed in terms of
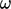 by
substituting
by
substituting 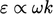 . Its form is due to the expansion of
. Its form is due to the expansion of 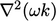 in the diffusion term
by Eq. (2.74b
).
in the diffusion term
by Eq. (2.74b
).
The cross-diffusion term makes the 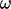 equation more
equivalent to
equation more
equivalent to  , and thus independent of freestream values.
, and thus independent of freestream values.
Stress limiter
The original  and
and  models are known to
delay or suppress flow separation under adverse pressure gradients
(described in Sec. 6.5
). Under such
conditions the ratio of the production to dissipation of
models are known to
delay or suppress flow separation under adverse pressure gradients
(described in Sec. 6.5
). Under such
conditions the ratio of the production to dissipation of
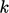 can be significantly higher than unity. The calculated
can be significantly higher than unity. The calculated 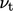 from
Eq. (7.39
) is excessively high, causing
an over-prediction of shear stress
from
Eq. (7.39
) is excessively high, causing
an over-prediction of shear stress  .
.
The problem is alleviated by limiting the shear
stress, based on the assumption it is proportional to  in the
boundary layer, i.e.
in the
boundary layer, i.e.
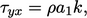 where
where 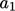 is a constant. A stress limiter is implemented through a
modification to the calculation of
is a constant. A stress limiter is implemented through a
modification to the calculation of 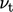 :
:
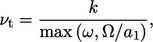 |
(7.43) |
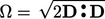 is a 3D representation of
is a 3D representation of 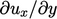 .
.
Standard models
Different versions of the  model are well
catalogued in the Turbulence
modeling resource,
NASA Langley Research Center, https://turbmodels.larc.nasa.gov.
model are well
catalogued in the Turbulence
modeling resource,
NASA Langley Research Center, https://turbmodels.larc.nasa.gov.
Today, there are arguably two “standard”
 models, First, the
models, First, the  -
- SST model,18 (SST = shear stress transport) which emerged
as a popular choice in CFD over recent decades.
SST model,18 (SST = shear stress transport) which emerged
as a popular choice in CFD over recent decades.
It combines the  model near the wall
with
model near the wall
with  (expressed in terms of
(expressed in terms of 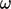 ) in the freestream, by
applying blending functions
to model coefficients, the cross-diffusion term and the stress
limiter.
) in the freestream, by
applying blending functions
to model coefficients, the cross-diffusion term and the stress
limiter.
Secondly, the 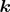 -
- 2006 model19 applies the cross-diffusion term and stress
limiting to the original
2006 model19 applies the cross-diffusion term and stress
limiting to the original  model. The terms are applied using
switches so that the model
maintains its simplicity, without the need for blending
functions.
model. The terms are applied using
switches so that the model
maintains its simplicity, without the need for blending
functions.


