7.13 Thermal boundary layers
In a turbulent boundary layer, the distribution
of temperature is similar to velocity, with the viscous and
intertial sub-layers, separated by a buffer layer, as discussed in
Sec. 7.4
.
By analogy with  , Eq. (7.10
), we define friction temperature
as
, Eq. (7.10
), we define friction temperature
as

|
(7.49) |
The wall layer is then described by a dimensionless temperature
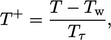
|
(7.50) |
where
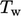
is the fluid temperature at the wall. Ignoring heat
generation by viscous stresses, the profile in the viscous sub-layer
is described by the relation
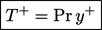
|
(7.51) |
The profile in the inertial sub-layer is commonly described by a log
law for
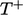
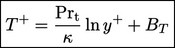
|
(7.52) |
The derivation of Eq. (
7.51
) and Eq. (
7.52)
assumes a constant heat flux across the profile, equating to
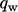
at
the wall. In the viscous sub-layer, the heat flux is laminar so
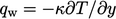
and
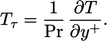
|
(7.53) |
This equation integrates between

at a distance

from the wall to
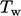
at the wall, to yield Eq. (
7.51). In
the inertial layer, the heat flux is assumed turbulent
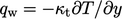
and
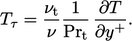
|
(7.54) |
Combining Eq. (
6.24),
Eq. (
7.9)
and Eq. (
7.15
) yields the ratio
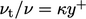
.
Substituting in Eq. (
7.54
) and integrating then
leads to Eq. (
7.52
) where
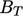
is the constant of
integration.
The constant 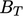 is generally
considered to be a function of
is generally
considered to be a function of 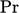 . A reasonable
approximation for this function is
. A reasonable
approximation for this function is
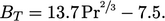
|
(7.55) |
Another function, commonly used in thermal wall functions, is
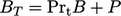
,
where
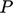
is the function of
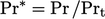
:
![h 3=4 i P = 9:24 (Pr ) 1 [1 + 0:28 exp ( 0:007Pr )]: \relax \special {t4ht=](img/index3375x.png)
|
(7.56) |
The expression for
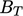
uses the coefficient
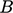
from
Eq. (
7.11).
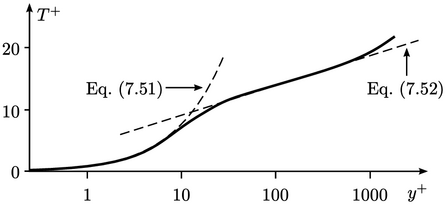
These constants of integration are sometimes subsumed within the
log function as a coefficient “
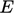
” in the log law
expressions, as the footnote on page
483
explains.
 , Eq. (7.10
), we define friction temperature
as
, Eq. (7.10
), we define friction temperature
as
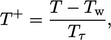
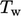 is the fluid temperature at the wall. Ignoring heat
generation by viscous stresses, the profile in the viscous sub-layer
is described by the relation
is the fluid temperature at the wall. Ignoring heat
generation by viscous stresses, the profile in the viscous sub-layer
is described by the relation
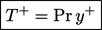
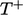
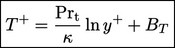
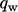 at
the wall. In the viscous sub-layer, the heat flux is laminar so
at
the wall. In the viscous sub-layer, the heat flux is laminar so
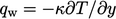 and
and
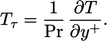
 at a distance
at a distance
 from the wall to
from the wall to 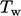 at the wall, to yield Eq. (7.51). In
the inertial layer, the heat flux is assumed turbulent
at the wall, to yield Eq. (7.51). In
the inertial layer, the heat flux is assumed turbulent 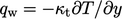 and
and
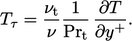
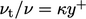 .
Substituting in Eq. (7.54
) and integrating then
leads to Eq. (7.52
) where
.
Substituting in Eq. (7.54
) and integrating then
leads to Eq. (7.52
) where 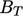 is the constant of
integration.
is the constant of
integration.
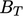 is generally
considered to be a function of
is generally
considered to be a function of 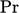 . A reasonable
approximation for this function is20
. A reasonable
approximation for this function is20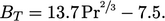
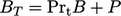 ,
where
,
where 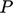 is the function of
is the function of 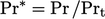 :21
:21
![h 3=4 i P = 9:24 (Pr ) 1 [1 + 0:28 exp ( 0:007Pr )]: \relax \special {t4ht=](img/index3375x.png)
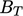 uses the coefficient
uses the coefficient 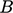 from
Eq. (7.11).
These constants of integration are sometimes subsumed within the
log function as a coefficient “
from
Eq. (7.11).
These constants of integration are sometimes subsumed within the
log function as a coefficient “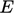 ” in the log law
expressions, as the footnote on page 483
explains.
” in the log law
expressions, as the footnote on page 483
explains.

