7.1 The k-epsilon turbulence model
The  model
(k-epsilon) was the first turbulence model to be widely adopted for
a variety of flows in CFD.2 It is one of a family of two equation models which solve two
transport equations, one usually for
model
(k-epsilon) was the first turbulence model to be widely adopted for
a variety of flows in CFD.2 It is one of a family of two equation models which solve two
transport equations, one usually for 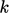 and one for another
variable, often a dissipation rate. These models are the industry
standard for CFD.
and one for another
variable, often a dissipation rate. These models are the industry
standard for CFD.
The  model combines the transport equations for
model combines the transport equations for
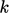 and
and 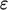 ,
Eq. (6.28
) and Eq. (6.32
) respectively, which are
reproduced below assuming
,
Eq. (6.28
) and Eq. (6.32
) respectively, which are
reproduced below assuming 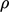 = constant and replacing material
derivatives in conservative form as in Eq. (2.26
).
= constant and replacing material
derivatives in conservative form as in Eq. (2.26
).
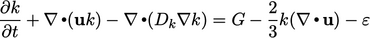 |
(7.1) |
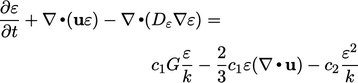 |
(7.2) |
The standard model coefficients are
 |
(7.3) |
The model can be deployed in a steady flow
solution, setting the local time derivatives to zero, e.g. 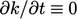 . It can also form part
of a transient solution to capture unsteady features such as vortex
shedding.
. It can also form part
of a transient solution to capture unsteady features such as vortex
shedding.
The model uses a momentum equation in
ensemble-averaged form, e.g. Eq. (6.26
), using  calculated from
updated
calculated from
updated  and
and 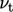 according to Eq. (6.27
).
according to Eq. (6.27
).
The model equations are added to the end of the main loop in the steady and transient algorithms from Sec. 5.12 or Sec. 5.21 , respectively. The figure below shows the additions to the transient algorithm, starting from the momentum corrector step.

Following the momentum and flux correctors,
 can be updated, e.g. for
non-Newtonian models where
can be updated, e.g. for
non-Newtonian models where 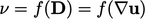 .
. 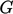 and
and 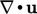 are calculated and
stored for source terms in both the
are calculated and
stored for source terms in both the 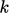 and
and 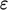 equations. Those
equations are then solved, followed by an update to
equations. Those
equations are then solved, followed by an update to 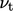 , and subsequently
, and subsequently
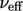 .
.

