7.3 Inlet turbulence
Expressions are presented in Sec. 7.2
to estimate inlet and
initial values of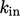 
and 
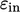. They include parameters 
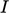and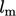 
which must
themselves be estimated sufficiently accurately to calculate
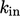and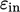 
reliably.
The values of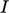 
and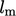 
at domain inlets
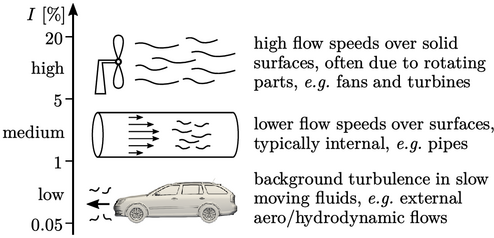
depend on the flow conditions upstream of the inlet. The figure below
shows typical ranges of intensity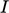 
for different upstream
flow conditions.
A medium intensity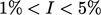 
is most commonly
specified in CFD problems, in particular for internal flows. For
these flows, 
can be calculated from a power-law function of
,
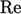fitted to measurements at the central axis in fully developed flow
along a smooth-wall pipe, according to4
 |
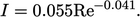(7.7) |
at the centre axis of a pipe, see Sec. 6.12
, can be used in
conjunction with 
from of Eq. (7.7
). For ducts and
channels of non-circular cross-section,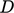 
can be calculated by
,
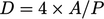where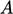 
is the cross-sectional area and 
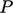is the perimeter
length. For a partially filled pipe or duct, 
corresponds to the
wetted region where the fluid is in contact with the boundary.
For wall-bounded flows with a boundary layer of
thickness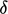 
, an estimate of 
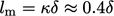is often used. This relation (see also
Sec. 6.12
) requires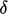 
to be estimated,
e.g. from the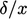 
expression for
a turbulent layer at the end of Sec. 6.4
.
Verifying turbulent viscosity
Combining Eq. (7.4
), Eq. (7.6
) and Eq. (6.31
) gives the following
expression for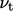 
in terms of length 
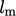and velocity
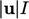scales:
 |
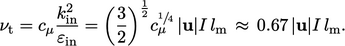(7.8) |
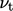need to be realistic. Realistic values usually fall within
the range of molecular viscosities 
for common fluids at standard temperature shown below.
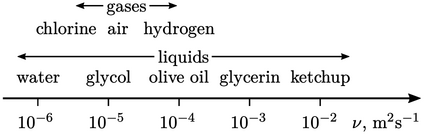
The range is presented in terms of kinematic viscosity 
which governs the
rate of momentum
diffusion, e.g. the rate of growth of boundary
layers. By contrast, forces
are governed by dynamic viscosity 
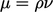, which make liquids
“feel” more viscous.
