6.15 Summary of turbulence
- Turbulence is a spatially complex distribution of vorticity which advects itself in a chaotic manner, Sec. 6.2 .
- Vorticity is mostly generated at solid boundaries and evolves by advection, diffusion and stretching/compression, Sec. 6.3 .
- Boundary layers are thus the main source of vorticity for turbulence, Sec. 6.4 .
- Turbulence occurs when instabilities cause the vorticity to become chaotic, characterised by Reynolds Number, Sec. 6.1 .
Scales of turbulence
- Length and time scales of turbulent eddies initially relate to the characteristic scales of the generated vortices, e.g. by shedding, Sec. 6.5 .
- The eddies become progressively smaller until they reach a size where the dissipation of their kinetic energy is significant, Sec. 6.6 .
- The process of eddy breakup involves a cascade of kinetic energy from larger to smaller eddies in which eddy structures become increasingly isotropic, Sec. 6.7 .
Simulating turbulence
- The Kolmogorov microscales represent the smallest scales of turbulence at which eddies die out by viscous dissipation.
- They are surprisingly small, e.g. a factor of
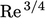 separates the length
scales of the largest and smallest eddies.
separates the length
scales of the largest and smallest eddies. - Usually, it is prohibitively costly to capture the smallest scales in a CFD simulation, Sec. 6.8 .
- Large-eddy simulation captures the large eddies, while using modelling for the unresolved scales.
- Reynolds-averaged simulations provide faster solutions by solving equations for averaged field variables, Sec. 6.9 .
- The averaged momentum equation includes the Reynolds stress which requires modelling.
Turbulence modelling concepts
- Momentum exchange at the molecular scale is characterised by viscosity and kinetic theory provides good quantitative predictions of viscosity for gases, Sec. 6.10 .
- Comparing the random motion of eddies in a turbulent fluid with particles at a molecular scale, Boussinesq introduced the concept of eddy viscosity, Sec. 6.11 .
- Eddy viscosity is not a fluid property but is proportional to a characteristic speed and length scale of the turbulence; models are required which represent each of these scales.
- The speed scale is represented by turbulent
kinetic energy
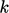 , described by a transport equation Eq. (6.28
), Sec. 6.13
.
, described by a transport equation Eq. (6.28
), Sec. 6.13
. - The
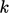 -equation includes a term for its rate of
dissipation
-equation includes a term for its rate of
dissipation 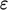 ; a transport equation for
; a transport equation for 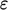 , e.g. Eq. (6.32
), provides a model for that
term — which also represents the length scale of turbulence,
Sec. 6.14
.
, e.g. Eq. (6.32
), provides a model for that
term — which also represents the length scale of turbulence,
Sec. 6.14
. - The concept of mixing length to characterise the length scale of turbulence provides additional modelling, particularly for the near-wall region, Sec. 6.12 .
Notes on CFD: General Principles - 6.15 Summary of turbulence

