6.11 Turbulent mixing
Turbulent flow is characterised by significant mixing of fluid eddies as the Reynolds experiment in Sec. 6.1 shows. CFD simulations generally need to accommodate turbulent mixing since it influences the diffusion of mass, momentum and energy. While the fluid mixing by mass diffusion itself can be important, the effect on momentum diffusion is often critical because it impacts the calculation of viscous forces and, thus, the flow itself.
Eddy viscosity
Boussinesq was the first to devise a model for turbulence. He recognised the similarity between the random motion of both eddies in a turbulent fluid and particles at a molecular scale.

By analogy to kinetic theory in
Sec. 6.10
, shear stresses due to
turbulence are caused by the net momentum, tangential to a plane,
due to the motion of eddies. Boussinesq related this shear
stress to the
velocity gradient through an eddy
viscosity 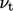 .14
.14
He presented the turbulent stress 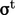 in tensor form,
including a pressure. Kinetic theory relates pressure to fluctuations15 in
particle velocity
in tensor form,
including a pressure. Kinetic theory relates pressure to fluctuations15 in
particle velocity 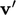 by
by 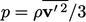 ; the kinetic energy associated with the
fluctuations is
; the kinetic energy associated with the
fluctuations is 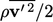 . Applying the same argument to velocity fluctuations
. Applying the same argument to velocity fluctuations
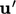 due to turbulence, leads to a turbulent “pressure”
due to turbulence, leads to a turbulent “pressure”  , where
, where
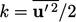 is
the turbulent kinetic
energy per
unit mass.
is
the turbulent kinetic
energy per
unit mass.
By analogy with the Newtonian fluid model
Eq. (2.41
), the eddy viscosity model of
Boussinesq, incorporating  , is
, is
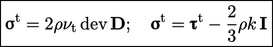 |
(6.20) |
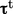 is the viscous component of Reynolds stress and
is the viscous component of Reynolds stress and 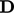 is the deformation rate tensor defined in
Eq. (2.33
). Inevitably
Eq. (6.20
) and Eq. (2.41
) closely resemble one another.
is the deformation rate tensor defined in
Eq. (2.33
). Inevitably
Eq. (6.20
) and Eq. (2.41
) closely resemble one another.
The model of Eq. (6.20)
requires some means of calculating 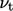 . Kinetic theory gives
a quantitative prediction of
. Kinetic theory gives
a quantitative prediction of  in Eq. (6.19
) which led Boussinesq
to hypothesise that
in Eq. (6.19
) which led Boussinesq
to hypothesise that  , where
, where 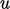 and
and 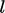 are a representative
speed and length, respectively, with the speed
are a representative
speed and length, respectively, with the speed 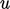 relating to
relating to
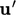 due to turbulence.
due to turbulence.
The turbulent viscosity can also be expressed as
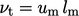 by
absorbing the constant of proportionality within a characteristic
speed
by
absorbing the constant of proportionality within a characteristic
speed  and a mixing length
and a mixing length
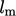 ,
discussed in Sec. 6.12
.
,
discussed in Sec. 6.12
.
Eddy viscosity and mixing length are useful concepts in turbulence modelling. However, it should be recognised that there are limitations in the analogy with kinetic theory, e.g.:
- momentum is exchanged between submicroscopic particles through intermittent, discrete collisions, compared to the continuous interaction between eddies;
- the magnitude of random particle motions is generally equal in all directions, whereas the level of turbulent fluctuations can sometimes vary significantly with direction.

