6.13 Turbulent kinetic energy
The Reynolds stress 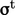 in the
ensemble-averaged momentum conservation Eq. (6.15
) can be decomposed into
viscous and pressure components. The turbulent pressure term,
in the
ensemble-averaged momentum conservation Eq. (6.15
) can be decomposed into
viscous and pressure components. The turbulent pressure term,
 ,
is commonly subsumed within pressure
,
is commonly subsumed within pressure 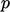 , to give
, to give
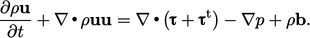 |
(6.25) |
 is modelled as a
Newtonian fluid Eq. (2.41
) and
is modelled as a
Newtonian fluid Eq. (2.41
) and  by the eddy viscosity
model Eq. (6.20
) to give
by the eddy viscosity
model Eq. (6.20
) to give
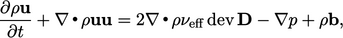 |
(6.26) |
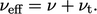 |
(6.27) |
 .
.
Averaging the momentum equation and introducing
the eddy viscosity model creates one additional unknown
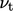 .
Additional models are required for
.
Additional models are required for 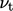 to close the system of
equations.
to close the system of
equations.
By considering 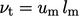 from
Sec. 6.11
, the model for
from
Sec. 6.11
, the model for
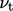 is
typically decomposed into components representing velocity and
length scales,
is
typically decomposed into components representing velocity and
length scales, 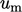 and
and 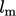 respectively.
respectively.
The scale of 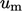 corresponds to
turbulent fluctuations
corresponds to
turbulent fluctuations 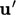 , so it is reasonable to assume that
, so it is reasonable to assume that
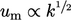 .
Since the field
.
Since the field 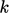 is representative of the
is representative of the 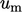 component of
component of
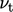 ,
it is commonly adopted within turbulence models based on
,
it is commonly adopted within turbulence models based on
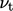 .
Also, it is well captured by a suitable conservation equation.
.
Also, it is well captured by a suitable conservation equation.
Transport of turbulent kinetic energy
Conservation of turbulent kinetic energy
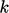 can be written as:
can be written as:
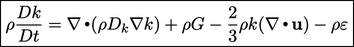 |
(6.28) |
 is
is
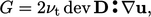 |
(6.29) |
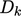 is the effective diffusivity for
is the effective diffusivity for 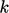 . The equation is
derived in a manner similar to Eq. (2.56
) for conservation of
specific internal energy
. The equation is
derived in a manner similar to Eq. (2.56
) for conservation of
specific internal energy  , by (ensemble) averaging the separate
energy contributions from
, by (ensemble) averaging the separate
energy contributions from 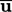 and
and 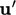 . While
. While  includes the
kinetic energy of molecular motion,
includes the
kinetic energy of molecular motion, 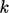 is the equivalent for
eddy motion.
is the equivalent for
eddy motion.
In Eq. (2.56
), energy from bulk motion
is passed to the submicroscopic scale as heat by 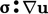 . In Eq. (6.28), it is
converted to turbulent
energy by
. In Eq. (6.28), it is
converted to turbulent
energy by 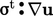 using Boussinesq’s
using Boussinesq’s 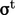 from
Eq. (6.20
). The shear component
from
Eq. (6.20
). The shear component
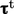 provides the non-recoverable
provides the non-recoverable  in Eq. (6.28) and
the second (
in Eq. (6.28) and
the second (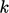 ) term yields
) term yields 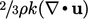 .
.
While 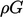 transfers kinetic energy from the bulk flow
to
transfers kinetic energy from the bulk flow
to 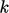 , the final term
, the final term 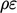 transfers
transfers  on to
on to  as dissipated
heat. Here,
as dissipated
heat. Here, 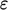 is the turbulent
dissipation rate per unit mass from
in Sec. 6.6
which, from an
ensemble-averaged derivation of Eq. (6.28),
is
is the turbulent
dissipation rate per unit mass from
in Sec. 6.6
which, from an
ensemble-averaged derivation of Eq. (6.28),
is
 |
(6.30) |
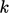 is represented by
is represented by 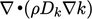 , where
, where 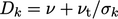 . This represents
diffusion by both molecular and turbulent motions and interactions,
including an adjustable coefficient
. This represents
diffusion by both molecular and turbulent motions and interactions,
including an adjustable coefficient 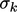 which is usually set
to 1.
which is usually set
to 1.
The 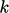 equation goes part of the way to closing our
system of equations. However, it introduces an additional unknown,
equation goes part of the way to closing our
system of equations. However, it introduces an additional unknown, 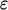 , and the model for
, and the model for
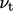 still requires length scale
still requires length scale
 .
.

