6.3 Vorticity transport
For an incompressible fluid (with other simplifying assumptions), vorticity obeys the transport equation , Eq. (6.2 ). This is a typical advection-diffusion equation, similar to Eq. (2.65 ) for heat, which is expressed in terms of the local time derivative and advection in conservative form by
 |
(6.1) |
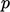. This is in contrast with conservation of
(linear) momentum which can redistribute a perturbation in
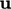instantaneously across all the domain through 
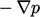, as discussed in
Sec. 2.22
.
Instead, like heat, vorticity evolves locally only, with a range of influence limited by advective and diffusive transport, as discussed on page 126 .
Advection of vorticity is clearly illustrated by the smoke ring shown in Sec. 2.11 . Diffusion occurs by viscous torques transferring angular momentum between fluid elements.
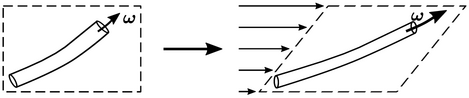
The source of vorticity,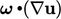 
is due to vortices
changing shape under the influence of a velocity gradient
.
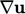If a vortex is stretched, e.g. under shear as shown above, its
radius decreases, so angular velocity, and thus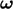 
, increases.
Similarly,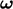 
decreases if the vortex is compressed.
The vorticity transport equation
For incompressible flow with constant
(and zero, or constant, body force), vorticity obeys the following
transport equation:
 |
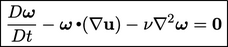(6.2) |
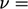constant and
ignoring body forces, Eq. (2.49
).
Noting that 
due to Eq. (2.46
) leads to
 |
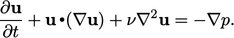(6.3) |
) of
Eq. (6.3
) combined with the vorticity definition
Eq. (2.37
). The first term is
.
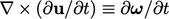Replacing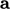 
and 
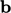by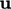 
in
Eq. (2.72d
) and applying
Eq. (2.37
) gives
 |
(6.4) |
 |
(6.5) |
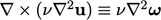by Eq. (2.74f
). The curl of the fourth
term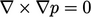 
by Eq. (2.75a
).
Combining all the terms and applying the material
derivative Eq. (2.14
), 
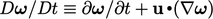to
Eq. (6.5
), leads to Eq. (6.2
).
