6.4 Boundary layers
Boundary layers4 are
regions of fluid formed along solid boundaries in which the velocity
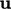varies: from zero at the boundary (no-slip condition,
Sec. 4.4
); to a value largely unaffected
by the proximity of the boundary, determined by the flow
conditions.
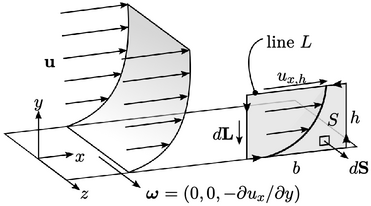
The figure above shows a boundary layer for flow
in the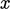 
-direction at speed 
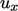, along a flat solid boundary oriented in the
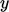-normal direction. At the boundary surface, the vorticity
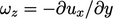is
significant.
Vorticity can be shown over a planar section of
the boundary layer of width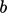 
and height
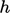(above, right). Applying Stokes’s theorem, Eq. (2.39
), the integral =
along the upper line (with zero along the wall and the verticals
sides). The average vorticity over plane area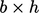 
is therefore
.
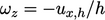Boundary layers are the main source of vorticity
for turbulence. Turbulence occurs when instabilities, e.g. induced by roughness of the
boundary surface, cause the vorticity to become chaotic, sustained
by a sufficiently high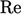 
.
The growth of boundary layers is related to
vorticity transport. For flow over a flat plate, vorticity generated
at the leading edge is advected by the flow, while diffusing away
from the plate.
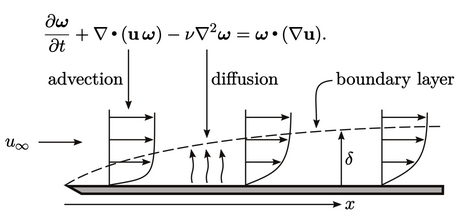
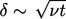in time 
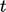, see
Sec. 2.22
. In that time, it is advected
a distance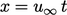 
, where 
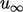is the freestream flow speed. Comparing the
distances over the same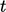 
, the boundary layer thickness is
 |
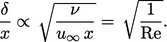(6.6) |
is suitable for laminar boundary layers, with coefficient
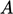depending on the definition of 
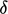. Data and analysis,
including e.g. the Blasius
solution5,
indicate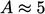 
in the case of the “99% thickness”, i.e. the distance from the wall where
velocity reaches 99% of its asymptotic value.
In turbulent boundary layers, the diffusion
front advances more rapidly due to mixing, see Sec. 6.11
. As a result,
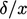is
relatively insensitive to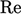 
, e.g. the analytical solution
,
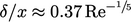based on a one-seventh (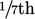
) power law for the velocity profile.
