6.10 The nature of viscosity
Before discussing turbulence further, it is useful to examine the origins of viscosity. Viscosity is introduced in Sec. 2.12 of this book as part of the Newtonian constitutive model. The model was originally phenomenological, but was later derived directly from kinetic theory which describes a gas as a number of submicroscopic particles, e.g. atoms or molecules, in random motion.
The kinetic view of viscosity imagines a fluid in
two dimensions, 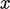 and
and 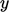 , subjected to a shear force in the
, subjected to a shear force in the 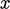 -direction.
Although the mean flow is in the
-direction.
Although the mean flow is in the 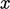 -direction, particles
move in the
-direction, particles
move in the 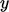 -direction due to random fluctuations with a
mean speed
-direction due to random fluctuations with a
mean speed  .
.
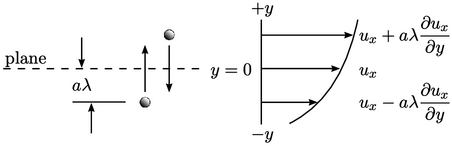
Consider a plane at 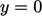 . A particle will pass
through the plane if its path towards it is not interrupted by a
collision which sends it moving away from the plane. Particles
passing through the plane arrive from an average distance
. A particle will pass
through the plane if its path towards it is not interrupted by a
collision which sends it moving away from the plane. Particles
passing through the plane arrive from an average distance
 ,
where
,
where  is some factor of the average distance travelled by a
moving particle between successive collisions, the mean free path
is some factor of the average distance travelled by a
moving particle between successive collisions, the mean free path  .
.
From kinetic theory, the mass flow rate of
particles passing through a surface of unit area 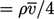 . The mean
. The mean
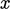 -velocity of particles crossing the plane from the
-velocity of particles crossing the plane from the
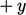 -direction is
-direction is 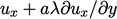 ; similarly from the
; similarly from the 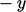 -direction, it is
-direction, it is
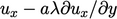 .
.
The net 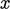 -momentum of the particles, positive on the
-momentum of the particles, positive on the
 side of the plane is then
side of the plane is then
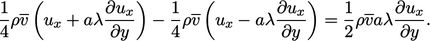 |
(6.16) |
The net momentum is equivalent to the shear
stress on the 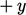 side of the plane,
side of the plane,  , as described in
Sec. 2.6
. By comparison with
Eq. (6.16
), the dynamic viscosity
, as described in
Sec. 2.6
. By comparison with
Eq. (6.16
), the dynamic viscosity
 in
terms of molecular properties. The kinematic viscosity is
in
terms of molecular properties. The kinematic viscosity is
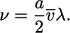 |
(6.17) |
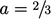 in Eq. (6.17
). It was later
recognised the average distance described by
in Eq. (6.17
). It was later
recognised the average distance described by  was larger due to
persistence of
velocities, i.e. a particle will sometimes maintain
a path towards the plane after a collision.
was larger due to
persistence of
velocities, i.e. a particle will sometimes maintain
a path towards the plane after a collision.
A more thorough analysis13 begins with the Boltzmann equation and applies the Chapman–Enskog expansion to first order in Knudsen number
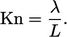 |
(6.18) |
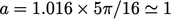 , leaving a simple expression for viscosity
which is
, leaving a simple expression for viscosity
which is
 |
(6.19) |

