6.7 Energy cascade
The process of large eddies becoming smaller is introduced in Sec. 6.6 . The process involves a transfer of kinetic energy from larger to smaller eddies, known as a the energy cascade.
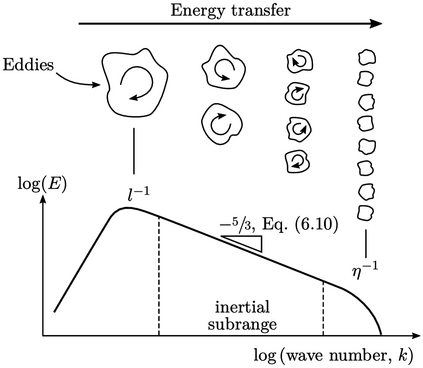
The variation in kinetic energy with eddy size
is often illustrated by the energy spectrum graph above. The
horizontal axis is wave number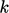 
,10
which represents the number of eddies per unit length, i.e. 
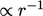where 
= eddy
size.
The cascade starts with the largest eddies of
size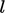 
with the highest level of turbulent kinetic energy per unit
mass (TKE). In the range,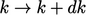 
, TKE = 
.
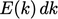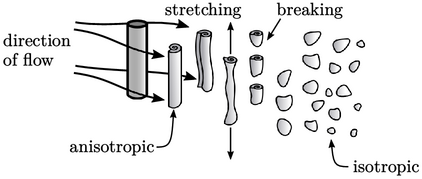
Large eddies are usually anisotropic due to the way turbulence is generated. For example, flow past a cylinder causes shedding of vortices whose shape are similar to the cylinder, i.e. longer in the direction of the cylinder axis.
Once moving through open space, eddies quickly
stretch, bend, rotate and break, so that quite soon they become
“blobs” of vorticity. The turn-over time, initially associated with
shedding, decreases with eddy-size — by a factor of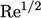 
at the smallest
scales, according to Eq. (6.9
). Any dominant
frequencies, e.g. those due
to shedding, are thereby quickly lost.
Kolmogorov’s hypothesis was that the turbulence
then becomes isotropic and
that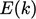 
is then only a function of 
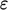and 
when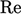 
is large. From
this hypothesis emerges his five-thirds law for the inertial subrange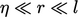 
 |
(6.10) |
for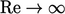 
. The exponents of 
and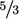 
are chosen to
match the dimensions of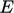 
which are 
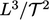, and noting
.
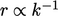Experimental data generally supports Eq. (6.10 ) — remarkably, given its simplicity.
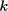, is commonly used in science
to denote wave number; it should not be confused with its
later use to denote turbulent kinetic
energy.