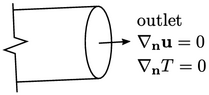
4.5 Inlets and outlets
A basic set of boundary conditions was introduced in Sec. 4.3 for incompressible subsonic flow.
At an inlet, fields are generally specified as fixed value. From a “physical” perspective, this is justified by the fact that disturbances propagate in the direction of flow so must be specified at the upstream boundary.
Advection requires interpolation of variables
from cell centres (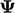
) to faces (
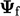). Some degree of
upwind interpolation, e.g.
as part of a limited scheme, is generally required. At a face at an
inlet patch there is no upwind cell, so values 
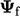must be specified at
inlet faces instead. From a “numerical” perspective, this justifies
the fixed value boundary condition at an inlet.
For incompressible, subsonic flow,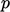 
is the exception.
A fixed gradient condition allows disturbances to propagate upstream
through the inlet as sound waves. The gradient condition is further
justified since there is no advection of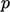 
, see
Eq. (2.48
), so no upwind
interpolation is required at the inlet patch faces.
At an outlet, the converse is then true:
fields are specified as fixed gradient condition, with the exception
of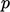 
which is fixed value. The outlet conditions ultimately dictate the
traction force combining Eq. (2.16
), Eq. (2.33
), Eq. (2.46
) and
Eq. (2.41
) as follows:
 |
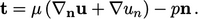(4.6) |
The standard condition applied to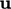 
is
.
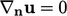By Eq. (4.6
), this results in a uniform
normal traction force
corresponding to the outlet pressure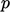 
. The traction force
tangential to the outlet
,
where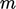 
is the tangential direction and 
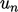is the normal
component of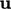 
.
Supersonic conditions
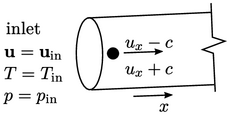
If the fluid is compressible and the flow speed
is supersonic at the inlet,
i.e. 
, waves can no longer
propagate outwards through the inlet boundary. When this occurs, a
fixed value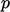 
must be specified at the inlet.
Similarly if the flow is supersonic at an outlet,
all disturbances propagate through the outlet. In that case,
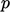cannot be specified, i.e. a
condition on the normal gradient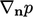 
is applied.
Some flow domains combine subsonic flow at the
inlet and supersonic flow at the outlet. When this occurs, a
gradient condition is required for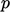 
at both boundaries,
leaving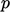 
under-specified. This problem is best overcome by moving the
outlet boundary sufficiently downstream for the flow to expand to
subsonic speed. This allows 
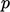to be specified through
a fixed value condition.
