4.3 Fundamentals of boundary conditions
The specification of boundary conditions is one of the most challenging tasks in setting up a CFD simulation. The range of possible boundary conditions is endless, to cover all of the potential applications and physics.
Setting boundary conditions is not an exact science but is guided by an basic specification using the fixed value (Dirichlet) and fixed gradient (Neumann) conditions introduced in Sec. 4.2 .
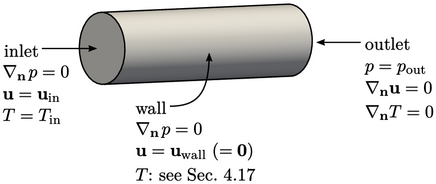
The figure above shows the basic specification
for 
, 
and 
for incompressible subsonic flow, e.g. described by Eq. (2.47
),
Eq. (2.48
) and
Eq. (2.65
).
The boundary conditions for 
and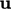 
require particular
attention since they are coupled. The conditions on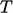 
are independent of
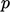and 
and are representative of other transported scalar fields,
e.g. turbulent kinetic
energy 
.
The specification for inlets and outlets summarises as:
- zero gradient on
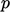at an inlet, fixed
value on other variables; - fixed value on
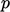at an outlet, zero
gradient on other variables.
Propagation of disturbances
A disturbance in a flow is simply any change from an equilibrium or steady solution. A disturbance at one location travels, or propagates, through the fluid.
The combination of boundary conditions at open
boundaries, i.e. those
excluding walls, relates to the propagation of disturbances. While
disturbances are transported by advection with the flow, they
propagate as waves at the speed of sound 
.
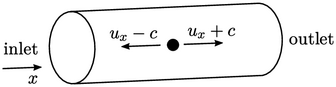
Sound waves can propagate disturbances against
the direction of flow if it is subsonic, i.e.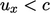 
. Disturbances must be
able to propagate outwards
through the inlet, which requires one variable not to be prescribed
at the inlet. Similarly, they must be able propagate inwards from the outlet, which requires
one variable to be prescribed at the outlet.
A pressure equation, combining mass and momentum
conservation, describes wave propagation. For an incompressible
fluid the wave speed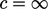 
, since Eq. (2.48
) contains no
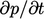term. A disturbance at any point influences
the solution everywhere in the domain instantaneously, as discussed
in Sec. 2.22
.
Pressure is then logically the variable on which
to specify the boundary conditions to support wave propagation.
Pressure is therefore: prescribed at the outlet, i.e. we specify fixed value condition;
not prescribed at the inlet, i.e. we specify a fixed gradient
condition, usually set to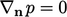 
.
