Notes on Computational Fluid Dynamics: General Principles

4.4 Wall boundaries

The no-slip condition is generally applied at a solid wall which is impermeable (assuming 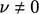). The condition is , where is the velocity of the wall, which is usually stationary with . The proof behind the no-slip condition is that it predicts a pressure drop along tubes of small diameter which matches experiments.³

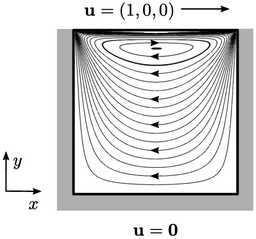
The 2D, lid-driven cavity is a flow problem in which no-slip conditions are applied at all boundaries. It provides insight into the boundary condition for 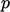at a wall. From Eq. (2.47 ) for an incompressible fluid, with 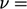 constant, the component normal to the domain boundary is

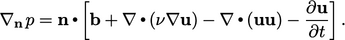(4.4)

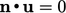At the solid wall boundary, the last 2 terms in Eq. (4.4) disappear since , reducing the gradient condition to

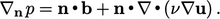(4.5)

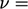The second term can be written ( constant) , so is only non-zero where there is flow normal to the boundary in its vicinity, e.g. at the corners of the cavity in our example. The term is usually small and its calculation involves extrapolation from the internal solution which often causes instability, so it is generally ignored.

A body force , e.g. gravity, is generally prescribed so it does not introduce instability. Where it is significant, it must be included in the boundary condition, i.e. .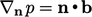

Otherwise, in the absence of a body force, we reach the standard form of boundary condition for pressure at a wall, .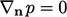

Fixing pressure

With only fixed gradient conditions on pressure at the boundary, the pressure value is not fixed at any point in solution domain. The solution is not unique, as shown in the 1D example below with gradient conditions at both ends.

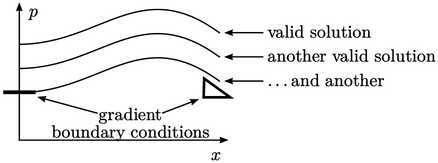
To achieve a unique solution, must then be fixed to a reference value 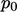at a reference cell in the domain. To achieve this, the diagonal coefficient 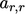is doubled and 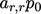is added to source , in the matrix equation 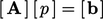described by Eq. (3.1 ). This minimal change “pins” the solution to in cell .

---

---