Notes on Computational Fluid Dynamics: General Principles

4.15 Inlet-outlet-velocity condition

The inlet-outlet condition was described in Sec. 4.10 , which switches between the zero gradient type for outflow and fixed value for inflow. The condition is not so suitable for velocity, e.g. at a free boundary, since it is requires an inlet velocity to be prescribed when inflow occurs.

The switching based on the flow direction is not a problem in itself. The flow direction comes from the sign of the flux , as noted in Eq. (4.12 ), which is determined by the solution of the pressure equation (part of pressure-velocity coupling described in Chapter 5 ).

The problem is instead that a value of velocity cannot be chosen in the case of inflow since the inflow speed is determined by the solution within the domain. This suggests a zero gradient type as a more suitable condition.

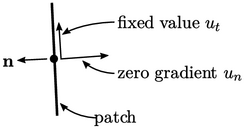
However, Sec. 4.3 discusses that all but one variable should be prescribed at a boundary with inflow. For velocity that variable could be its normal component, while a fixed value could still be applied to the tangential component.

The direction mixed type described in Sec. 4.14 provides the framework to implement this condition. A reference value 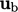is specified and the reference gradient is zero, i.e. .

The value fraction tensor is calculated as

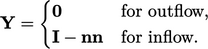(4.26)

The fixed value which is applied must be a velocity tangential to the boundary, which can be calculated by subtracting the normal component from a specified by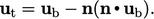

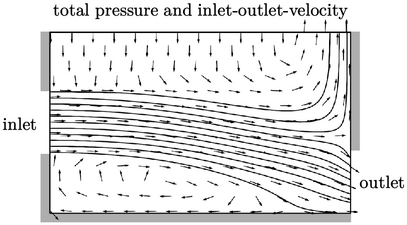
This inlet-outlet-velocity condition can be applied at the free boundary in the example from Sec. 4.6 . For free boundaries like this, 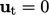is the only practical specification, which causes all inflow to be normal to the free boundary, as shown above.

The solution is clearly different to that using 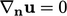shown on page 267 . There, the inflow direction is determined by the solution rather than prescribed. The solution with 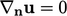may be more accurate but the inlet-outlet-velocity condition adheres better to the general principles of boundary conditions, so is likely to be more stable.

It becomes less contentious to set with the inlet-outlet-velocity condition as the boundary is moved further into the far field, where the flow is more quiescent.