4.16 Blended freestream condition
There is a class of problems in CFD that involve external flow around one or more solid bodies, e.g. a vehicle, wind turbine, buildings, etc.
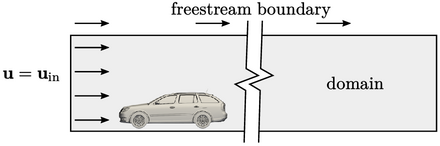
A solution domain is specified which includes
the solid body and extends some distance to a free boundary in the
far-field. A flow velocity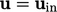 
is specified which can
be applied as a fixed value type at an inlet patch.
The far-field boundary requires attention. The
robust conditions at a free boundary for 
and 
are
inlet-outlet-velocity and total pressure described in
Sec. 4.15
and
Sec. 4.7
respectively.
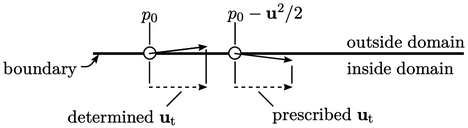
The inlet-outlet-velocity requires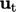 
to be
prescribed for inflow which may differ significantly from a determined
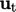when there is outflow. Solution accuracy depends on the suitability
of the prescribed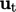 
.
The flow direction in the far-field can often be
close to tangential to the boundary, especially with a box-shaped
domain. If the flow at one face changes from outflow to inflow,
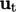suddenly changes to the prescribed fixed value and 
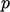decreases by
.
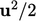Sometimes a pattern of switching can occur in adjacent faces and
repeated switching can slow the convergence of a solution.
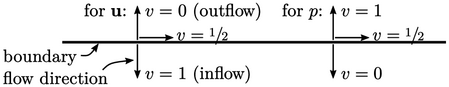
The blended
freestream condition is a mixed type with zero reference
gradient,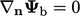 
, which modifies the value fraction 
as shown above. In the
limit that the flow direction is normal to the boundary, the
condition becomes the fundamental fixed value and zero gradient
types for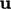 
and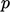 
.
Between these extremes, 
is blended linearly,
e.g. for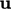 
by
 |
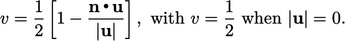(4.27) |
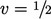for both 
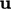and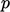 
for tangential flow.
At a boundary face,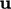 
may be directed
normal-inward, causing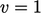 
by Eq. (4.27
). The condition can
then “lock” at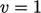 
, so to avoid this, the calculation can use a velocity
equating to the mean of the face and neighbour cell value,
i.e.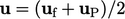 
.
Note that for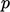 
, the value fraction is
calculated changing the sign of the second term in
Eq. (4.27
) i.e.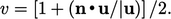 
The freestream conditions overcome the problem of switching to improve the convergence of solutions. Boundary velocities are determined, not prescribed, which seems to improve accuracy, e.g. in force calculations described in Sec. 8.4 and Sec. 8.6 .
