Notes on Computational Fluid Dynamics: General Principles

4.14 Direction mixed condition

In some cases, a boundary condition is sometimes needed which applies a different underlying type — fixed value or gradient — to different components of a non-scalar field.

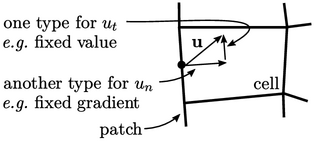
The condition is most readily applied to velocity 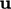, where different conditions are applied to its normal and tangential components to the patch, 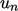and 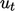respectively.

The direction mixed condition combines the mixed condition from Sec. 4.9 with the transform conditions of Sec. 4.11 . The mixed condition can be first expressed in the form of a general transform condition Eq. (4.13 ) as

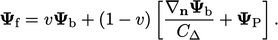(4.22)

In the direction mixed condition the value fraction is replaced by a transformation tensor , whose components are value fractions in the range 0 to 1, by

(4.23)

The value fraction tensor is set according to the requirements of the boundary condition which is derived from this direction mixed framework.

Imagine an example of at a face oriented with normal vector 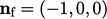, for which the condition is fixed gradient and 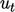is fixed value. The value fraction must be 1 in the tangential direction and 0 in the normal direction, which gives:

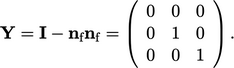(4.24)

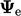The boundary condition is then implemented similarly to the symmetry and wedge conditions of Sec. 4.12 and Sec. 4.13 . First, is the calculated 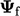using current 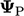by Eq. (4.23 ) and the explicit gradient is calculated from Eq. (4.17 ).

The factor 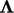corresponds to 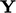. For a vector field, it is calculated, as in the symmetry condition in Eq. (4.19 ), by

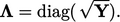(4.25)

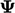For a tensor , the factor is 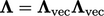, where 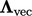are the coeffcients for a vector, as described for the symmetry condition in Sec. 4.12 .

The condition is implemented using value and gradient factors according to the transform condition, summarised in the table on page 284 . Any boundary condition which is based on this direction mixed condition then only requires a description of the 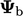, 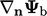and 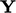parameters.