4.7 Total pressure condition
Sec. 4.6
concluded that the basic outflow
conditions —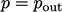 
and 
— are generally unstable for a free boundary
with both inflow and outflow.
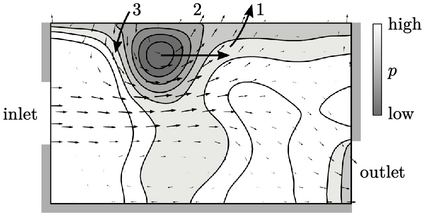
The conditions are unstable due to pressure fluctuations at the boundary, shown above. Flows oscillates in and out, shown by 3 stages, creating a vortex that travels from left to right:
- the pressure gradient, decreasing outward, causes outflow;
- the outflow speed increases causing the pressure gradient to change direction;
- inflow begins and the speed increases, until the pressure gradient changes direction, returning back to step 1.
The total pressure boundary condition improves the stability of solutions. It is a fixed value type, calculated according to:
 |
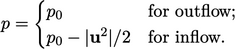(4.7) |
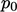, can be imagined as
the fluid pressure under quiescent conditions far from the free
boundary, which decreases as the fluid accelerates towards the
boundary. Note that Eq. (4.7
) is written for the
incompressible assumption, Eq. (2.47
), where
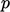and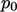 
are kinematic, i.e.
divided by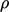 
.
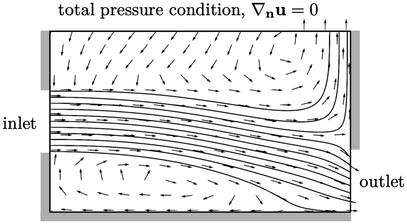
The solution using the total pressure condition
converges to the flow field shown above. The critical effect of this
boundary condition is that, the boundary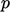 
decreases by
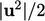as
the inflow speed 
increases. This reduces the pressure gradient driving
inflow, which moderates the increase in inflow speed, enabling it to
settle to a stable level.
Total pressure for high speed flow
The total pressure condition can be applied to
high-speed flow of a compressible gas. The calculation of
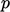for inflow is simply replaced with the 1D isentropic flow
equation,4
 |
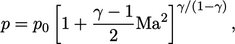(4.8) |
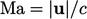and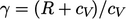 
.
