4.2 Fixed value and fixed gradient
In an equation for 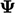 that is discretised to
form a matrix equation
that is discretised to
form a matrix equation 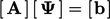 , there are two terms that include
properties interpolated to faces:
, there are two terms that include
properties interpolated to faces:
- an advection term of the form
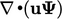 which is
discretised by Eq. (3.8
) in extensive
form (see Sec. 3.5
) as
which is
discretised by Eq. (3.8
) in extensive
form (see Sec. 3.5
) as  ;
; - a Laplacian term of the form
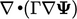 which is
discretised by Eq. (3.2
) in extensive
form as
which is
discretised by Eq. (3.2
) in extensive
form as 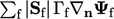 .
.
The advection term requires the value
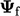 and Laplacian term requires the surface normal gradient
and Laplacian term requires the surface normal gradient
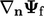 at
faces. When a face is part of a boundary patch, any gradient
at
faces. When a face is part of a boundary patch, any gradient
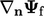 and/or value
and/or value 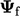 must be specified through boundary conditions.
must be specified through boundary conditions.
The fixed
value, or Dirichlet
condition,1 is the first type of boundary condition, where
the boundary value  is specified. For example, at an inlet patch, we might specify a temperature
is specified. For example, at an inlet patch, we might specify a temperature
 K of the fluid flowing into the domain.
K of the fluid flowing into the domain.
The fixed
gradient, or Neumann
condition,2
is the second
type, in which the gradient normal to the boundary 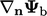 is specified (where
is specified (where
 ).
In many cases, the applied normal gradient is zero, which is a
common condition applied to many fields, including
).
In many cases, the applied normal gradient is zero, which is a
common condition applied to many fields, including 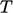 , at an
outlet patch, i.e. where the fluid flows out of the
domain.
, at an
outlet patch, i.e. where the fluid flows out of the
domain.

When an advection term is discretised, a fixed
value condition is applied by substituting the face value
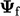 with the patch value
with the patch value 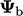 , i.e.
setting
, i.e.
setting 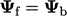 . When a fixed gradient
. When a fixed gradient 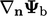 is specified, the face
value is expressed as follows, where
is specified, the face
value is expressed as follows, where 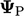 is the value in the
cell adjacent to each face:
is the value in the
cell adjacent to each face:
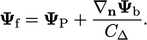 |
(4.2) |
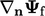 with the patch face normal gradient
with the patch face normal gradient 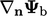 , i.e. setting
, i.e. setting 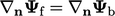 . When a fixed value
. When a fixed value
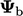 is
specified, the face normal gradient is expressed by
is
specified, the face normal gradient is expressed by
 |
(4.3) |

