4.1 Boundary mesh
Sec. 3.2 describes the computational mesh used by the finite volume method. It identifies a domain boundary by faces which are connected only to one cell. The boundary faces are grouped into patches, each under a unique name, corresponding to different regions of the boundary. Boundary conditions are then applied to each patch to provide a representative solution to the case of interest.
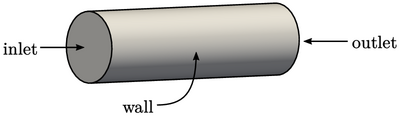
In the example of flow in a pipe, it would be logical to split the boundary into 3 patches in order to specify inflow, outflow and solid walls; and, inlet, outlet and wall would be logical names for these patches.
Patch geometric data
The geometry of a patch is described using face data described in Sec. 3.3 , including:
- the face area vector
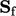, with area magnitude
and direction 
; - the face unit normal vector
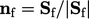; - the face centre
.
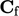The cell connected to each patch face is
denoted by the subscript “P”, e.g. the cell centre is denoted
.
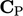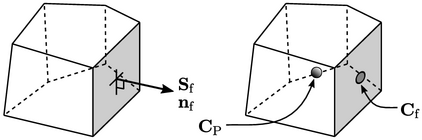
Patch deltas
Sec. 3.8
describes the “delta”
for each face as the vector connecting the centres of its owner and
neighbour cells.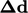 
is defined differently for a patch face since it has no
neighbour cell.
The delta is defined as the component of
in
the face normal direction. The surface gradient 
is orthogonal to
the face, which eliminates the error associated with
non-orthogonality, at the expense of
introducing a skewness error. Taking the
inner product with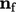 
gives the magnitude which is then multiplied by
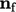to
assign the direction, i.e.
 |
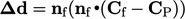(4.1) |
,
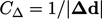as defined in Sec. 3.8
. The delta coefficient
,
representing “inverse distance”, is a critical parameter in the
discretisation of boundary conditions.
