4.9 Mixed fixed value/gradient
Sec. 4.8
concluded with a table of
factors for the contributions to coefficients of  and
and  for the fixed value
and fixed gradient boundary conditions.
for the fixed value
and fixed gradient boundary conditions.
It distinguishes between contributions for the discretisation of an advection term which requires values at faces, and the Laplacian term which requires the normal gradient.
A mixed
fixed value/gradient condition is defined by introducing a
value fraction  for which
for which
 |
(4.9) |
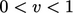 the condition operates in between fixed value and fixed
gradient. The mixed condition is simply implemented by blending the
fixed value and fixed gradient contributions by
the condition operates in between fixed value and fixed
gradient. The mixed condition is simply implemented by blending the
fixed value and fixed gradient contributions by  , as shown in the table
below.
, as shown in the table
below.
| factor | mixed |
|
|
|
| value internal | 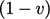 |
| value boundary |  |
| gradient internal | 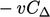 |
| gradient boundary |  |
|
|
|
This mixed condition provides the framework for
a boundary condition that can switch between a fixed value
 and fixed gradient
and fixed gradient 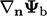 , by changing
, by changing  . Switching is often
based on flow direction,
. Switching is often
based on flow direction, 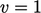 corresponding to inflow and
corresponding to inflow and 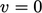 to outflow.
to outflow.
Some boundary conditions can operate in the range
of value fractions  . The Robin condition, described next, can also
be expressed as a mixed condition with varying
. The Robin condition, described next, can also
be expressed as a mixed condition with varying  .
.
Robin condition
The Robin condition5 combines the value and normal gradient at the boundary through an expression:
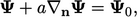 |
(4.10) |
 is a scalar coefficient with units of length and
is a scalar coefficient with units of length and 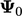 is some
constant value of
is some
constant value of 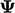 .
.
The Robin condition can be treated like the mixed
condition by relating 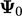 to a reference fixed value
to a reference fixed value 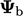 and gradient
and gradient
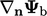 at
a boundary, according to
at
a boundary, according to 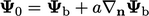 .
.
Substituting for 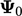 in Eq. (4.10) and making
in Eq. (4.10) and making
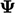 the subject of the equation gives:
the subject of the equation gives:
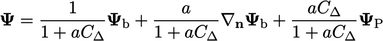 |
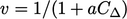 .
.
In this form, 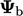 and
and 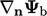 relate to the
limits
relate to the
limits 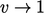 and
and 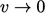 , respectively. Values can be selected in these limits
to represent the physics of the condition.
, respectively. Values can be selected in these limits
to represent the physics of the condition.
In many cases the reference gradient is
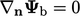 such that
such that 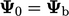 in Eq. (4.10
). For example a condition for
temperature
in Eq. (4.10
). For example a condition for
temperature 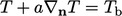 would tend to
would tend to 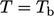 as
as  and
and 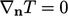 as
as
 .
.
The value fraction  includes
includes  , so the
condition operates “in the middle” between the fixed value and
gradient when
, so the
condition operates “in the middle” between the fixed value and
gradient when  is the same order of magnitude as the boundary cell
height.
is the same order of magnitude as the boundary cell
height.

