4.13 Axisymmetric (wedge) condition
There are some fluid flow problems for which the geometry is axisymmetric. Assuming the flow solution is axisymmetric, i.e. fields do not change in the circumferential direction, the computational mesh can be formed of a wedge-shaped slice of the flow geometry.
This type of mesh for axisymmetric solution contains one cell across the circumferential direction, which reduces the number of cells to two dimensions in the axial and radial directions.
This approach to axisymmetric solution introduces
a geometric error due the faces normal to the radial direction
being flat. This error reduces with decreasing wedge angle; in
practice, the error can be considered negligible for an angle of
1
.
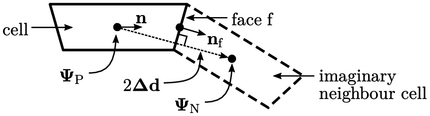
The wedge
boundary condition is applied to the two sloping side patches. It
transforms cell values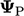 
to the patch faces using a rotational
transformation tensor 
by
 |
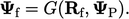(4.20) |
defines a rotation between the unit vector
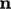in
the circumferential direction at the cell centre and the unit face
normal vector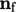 
by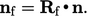 
The wedge condition uses the general transform
framework of Sec. 4.11
, with the explicit value
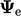calculated using current 
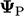from Eq. (4.20). The
explicit gradient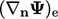 
is the boundary gradient 
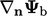calculated from
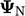in
an imaginary neighbour cell by
![C--- rn b = 2 [G(RN; P) P]; \relax \special {t4ht=](img/index1866x.png) |
(4.21) |
.
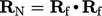The factor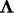 
is chosen to minimise
the gradient boundary coefficients (see Sec. 4.11
). The vector factor is
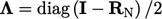where “
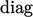” is defined in Sec. 4.12
.
For a tensor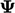 
, the factor is
,
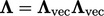where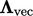 
are the coefficients for a vector, as described for the
symmetry condition in Sec. 4.12
.
Rotation tensor
The rotation tensor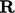 
between two
unit vectors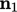 
and
can be calculated using the Euler-Rodrigues rotation
formula,6
 |
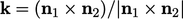and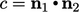 
.
