Notes on Computational Fluid Dynamics: General Principles

5.15 Conjugate gradient method

The solution to a matrix equation 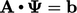by descent methods involves finding the minimum of the equation in quadratic form. This can be illustrated using the contours of the paraboloid describing the quadratic for the case with values 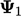and .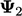

The search for the minimum involves a series of updates to 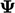of the form

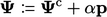(5.32)

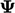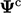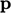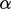where is the next update using latest (current) values . The column vector provides the direction of the line search towards the minimum; the scalar provides the magnitude of the line is that direction.

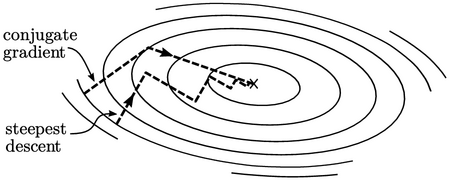
Steepest descent

The intuitive way to reach the minimum is to follow the direction of steepest descent. The method is fairly simple because the direction is defined by the negative of gradient of the quadratic form which is the residual .

The distance to “walk” is naturally until the lowest point is reached, corresponding to⁵

(5.33)

The method reaches the minimum point along a zigzag path where consecutive directions are orthogonal. The directions do not change and result in a larger number of very short steps, the more the paraboloid is stretched in one direction.

The conjugate direction

The conjugate gradient (CG) method chooses search directions that are conjugate with 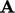. This means each new direction 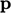corresponds to the previous one , satisfying

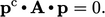(5.34)

This can be imagined as the directions being orthogonal with the stretch in the paraboloid removed. For 2 values, CG finds the minimum in 2 steps, rather than several zigzag steps.

CG provides the basis for practical matrix solvers for CFD, described in Sec. 5.16 . For a detailed explanation of the CG method, see the reference below.

---

---