8.2 Aspect ratio
The previous section mentioned cells of a mesh
that are longer in one direction than another. The parameter used
to describe this phenomenon is aspect ratio, defined as the ratio of
the longest to shortest dimensions,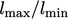 
, of a cell.
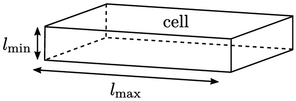
Meshes include cells with high aspect ratio for efficiency, by exploiting a prior understanding that the gradients in some flow properties e.g. shear stress, deformation rate and velocity, are much greater in one direction than others.
They are most commonly used to resolve the
boundary layers at walls. Greater mesh resolution is required
normal to the wall, where gradients are particularly high, than
tangential to the wall. The centre heights of cells adjacent to the
boundary need to be very small, corresponding to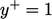 
.
In the aerofoil above, the aspect ratio is 1000 at the trailing edge. If those cells were replaced by ones with an aspect ratio of 1, with the same cell height, the number of cells would increase by a factor of 1000, illustrating the extent of the gains in efficiency.
Introducing high aspect ratio in one area of the
mesh causes problems elsewhere, however. The aerofoil example
maintains a high aspect ratio beyond the trailing edge, actually
increasing to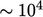 
further downstream. If the flow deviates from a
direction parallel to the long side of the high aspect ratio cells,
transient simulations then require very small 
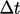to fall within
reasonable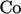 
limits. The mesh can be modified by abruptly reducing
the aspect ratio beyond the trailing edge, but this increases the
error associated with discretisation.
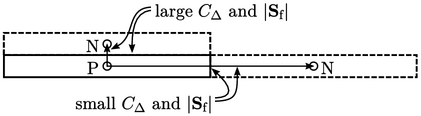
With Laplacian discretisation by
Eq. (3.2
) and
Eq. (3.5
), the matrix coefficients
include a factor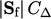 
. On a regular mesh, both 
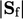and 
are larger for the
faces across the longest side of a high aspect ratio cell, than the
shortest side, by a factor equal to the aspect ratio. Matrix
coefficients can thereby differ by a factor of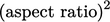 
.
The convergence of the pressure equation, dominated by the Laplacian derivative, is adversely affected, in particular with the CG-based matrix solvers. The GAMG solver fares much better because the agglomeration strategy is based on a progressive reduction in aspect ratio as discussed in Sec. 5.18 .
A matrix with a wide range of coefficient values
yields lower residual values 
, calculated from
Eq. (5.11
). In other words, for a given
, a
solution with high aspect ratio cells is less converged than one
without. Therefore, to maintain an equivalent level of convergence
with high aspect ratio cells, tolerance controls need to be
reduced, often by a few orders of magnitude.
