4.8 Numerical framework
The fixed value and fixed gradient conditions described in Sec. 4.2 can be combined to form a general numerical framework for boundary conditions.
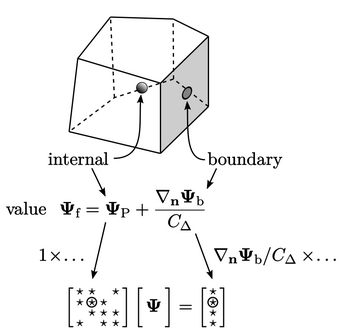
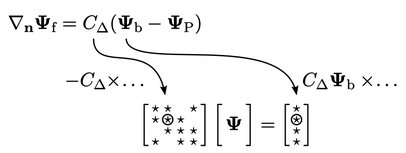
The contributions from the boundary conditions to
the matrix equation 
, by discretisation of advection and Laplacian
terms, can be generalised as:
- “internal” contributions to
, from terms
including the cell value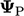 
; - “boundary” contributions to
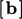, from terms
without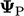 
.
The example above shows Eq. (4.2
) for the face
value, required at a boundary for advection discretisation, in the
case of a fixed gradient
boundary condition. The internal “factor” on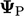 
is 1, which is
multiplied by 
for the contribution to the respective diagonal
coefficient in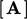 
, as in the example in Sec. 3.24
.
The boundary factor is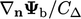 
, which is similarly
multiplied by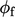 
for the contribution to 
.
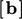For the fixed
value condition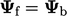 
with advection, the boundary factor is
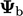and an internal factor is 0.
Laplacian discretisation requires the surface
normal gradient on the faces. A fixed gradient condition delivers an
equivalent boundary factor of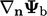 
to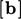 
and an internal
factor of 0.
,
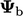the face normal gradient Eq. (4.3
) gives an internal
factor of 
and a boundary factor of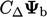 
. Both are multiplied
by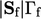 
in their contributions to 
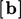and the diagonal coefficient of 
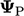in
,
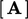as shown in the Laplacian discretisation in Sec. 3.24
.
The table below summarises: the “value” internal and boundary factors, contributing to the respective matrix coefficients with advection discretisation; and equivalent “gradient” factors relating to Laplacian discretisation. This provides a framework which can be extended to more complex conditions.
| term | factor | fixed value | fixed gradient |
|
|
|
|
|
| advection | value internal | 0 | 1 |
| advection | value boundary |  |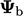
 |
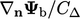| Laplacian | gradient internal |  |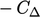
0 |
| Laplacian | gradient boundary |  |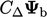
 |
|
|
|
|
|
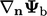