Notes on Computational Fluid Dynamics: General Principles

4.17 External wall heat flux

The boundary condition for temperature (or energy) dictates the heat transfer across a boundary. At a boundary that represents a solid wall, simple conditions can sometimes be applied. However, specialised boundary conditions are often required that control the heat flux across the boundary.

The fixed temperature is the simplest condition, setting a fixed value 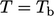. This condition provides an approximation for cases for a solid with high thermal mass, due to a large mass of material and high conductivity 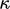, which helps to maintain constant .

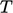Otherwise the boundary condition sets the heat flux normal to the boundary, derived from Eq. (2.54 ) by

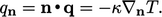(4.28)

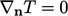Another simple condition is zero gradient . This is the adiabatic condition, corresponding to zero normal heat flux by Eq. (4.28 ), suitable when the solid is a thermally insulating material with a large mass and low .

Otherwise a fixed heat flux condition specifies an inward heat flux 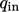as a fixed gradient type with a reference gradient by

(4.29)

Fixed heat transfer coefficient

Another way to specify the heat transfer at an external wall is by Newton’s law of cooling.⁷ This general law states the rate of heat loss of a body is directly proportional to the difference between the body temperature 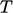and a surrounding, ambient temperature .

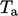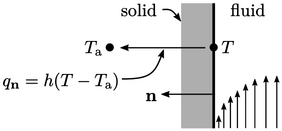
Applied as a boundary condition, 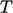is the fluid temperature at the boundary, and 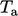a temperature some distance beyond the solid boundary. A heat transfer coefficient , with SI units 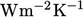, provides the constant of proportionality such that

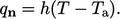(4.30)

Substituting Eq. (4.28 ) and rearranging gives an equation for the fixed heat transfer coefficient condition:

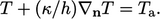(4.31)

The equation has the form of a Robin condition, Eq. (4.10 ), so can be implemented as described in Sec. 4.9 . The coefficient is typically characterised for the particular flow regime and solid boundary, by some estimate, experimental measurements or computer simulation.

---

---