5.11 Boundary fluxes
The equations in Sec. 5.10
are used to
compute the velocity 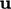 , flux
, flux  and pressure
and pressure 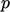 based on conservation
of mass and momentum. At boundaries, the flux corrector
Eq. (5.18
) must calculate
based on conservation
of mass and momentum. At boundaries, the flux corrector
Eq. (5.18
) must calculate
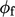 in
a manner consistent with
in
a manner consistent with 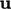 and
and 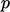 and their respective
boundary conditions.
and their respective
boundary conditions.
For example, at an impermeable stationary wall
the calculated flux must be 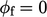 , consistent with the no-slip condition
, consistent with the no-slip condition
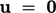 .
At boundary faces,
.
At boundary faces, 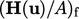 and
and 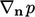 must be compatible to evaluate the correct
must be compatible to evaluate the correct
 according to Eq. (5.18
).
according to Eq. (5.18
).
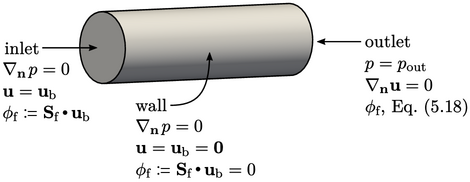
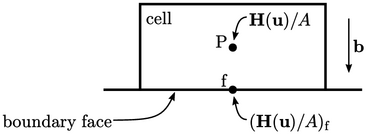
The figure shows the fundamental boundary
conditions from Sec. 4.3
and corresponding flux
evaluations. At the inlet and wall boundaries, 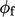 is directly assigned
from the boundary velocity
is directly assigned
from the boundary velocity  by
by 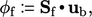 within the flux corrector Eq. (5.18
).
within the flux corrector Eq. (5.18
).
In the absence of body forces, the 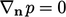 boundary
condition is commonly applied, as discussed in Sec. 4.4
. The flux
boundary
condition is commonly applied, as discussed in Sec. 4.4
. The flux 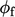 is then equivalent to
assigning
is then equivalent to
assigning 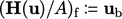 in Eq. (5.18
).
in Eq. (5.18
).
At the outlet, 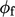 is not prescribed
since
is not prescribed
since 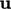 is not a fixed value condition. Instead,
is not a fixed value condition. Instead, 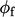 is evaluated from
Eq. (5.18
) using
is evaluated from
Eq. (5.18
) using 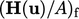 taken from cells
adjacent to the boundary and
taken from cells
adjacent to the boundary and 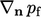 calculated on the
boundary.
calculated on the
boundary.
Fluxes with a body force
When a body force 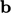 is present in the
momentum equation, the gradient condition for
is present in the
momentum equation, the gradient condition for 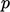 , e.g. at an inlet or wall, in principle
becomes
, e.g. at an inlet or wall, in principle
becomes 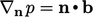 , as discussed in Sec. 4.4
. The precise details of the
boundary condition in fact depend on how
, as discussed in Sec. 4.4
. The precise details of the
boundary condition in fact depend on how  is incorporated within
the coupling algorithm, discussed below.
is incorporated within
the coupling algorithm, discussed below.
One approach, illustrated by the algorithm in
Sec. 5.10
, is to include
the body force 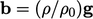 within
within 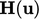 in Eq. (5.16
). In that case, the
assignment
in Eq. (5.16
). In that case, the
assignment 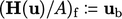 cannot be valid, so
cannot be valid, so 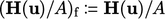 is adopted instead.
is adopted instead.
With 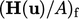 established, the
established, the  condition is
calculated based on the known
condition is
calculated based on the known 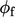 by inverting
Eq. (5.18
). This approach causes
by inverting
Eq. (5.18
). This approach causes
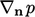 to
include a contribution from viscous stresses, as in
Eq. (4.5
), which may cause instability.
to
include a contribution from viscous stresses, as in
Eq. (4.5
), which may cause instability.
To avoid this problem, 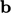 is omitted from
is omitted from
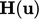 in
Eq. (5.16
), appearing instead as an
extra term in the other equations in Sec. 5.10
, e.g. the flux corrector
Eq. (5.18
) which becomes
in
Eq. (5.16
), appearing instead as an
extra term in the other equations in Sec. 5.10
, e.g. the flux corrector
Eq. (5.18
) which becomes
 |
(5.20) |
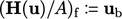 at boundaries where
at boundaries where 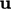 is fixed satisfies
Eq. (5.20
) when
is fixed satisfies
Eq. (5.20
) when
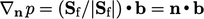 .
This is the condition ignoring viscous stresses described in
Sec. 4.4
.
.
This is the condition ignoring viscous stresses described in
Sec. 4.4
.

