[version 13][version 12][version 11][version 10][version 9][version 8][version 7][version 6]
4.5 Numerical schemes
The fvSchemes dictionary in the system directory sets the numerical schemes for terms, such as derivatives in equations, that are calculated during a simulation. This section describes how to specify the schemes in the fvSchemes dictionary. Details of the schemes are described in Chapter 3 of Notes on Computational Fluid Dynamics: General Principles.
The aim for fvSchemes is to provide an unrestricted choice of schemes
to the user for everything from derivatives, e.g. gradient 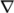 , to interpolations of
values from one set of points to another. OpenFOAM uses the
finite volume method so spatial derivatives are based on Gaussian
integration which sums values on cell faces, which must be
interpolated from cell centres. The user has a wide range of
options for interpolation schemes, with certain schemes being
specifically designed for particular derivative terms, especially
the advection divergence
, to interpolations of
values from one set of points to another. OpenFOAM uses the
finite volume method so spatial derivatives are based on Gaussian
integration which sums values on cell faces, which must be
interpolated from cell centres. The user has a wide range of
options for interpolation schemes, with certain schemes being
specifically designed for particular derivative terms, especially
the advection divergence 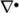 terms.
terms.
The set of terms, for which numerical schemes
must be specified, are subdivided within the fvSchemes dictionary into the categories below, using
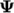 as
an example field variable.
as
an example field variable.
- timeScheme: first and second time derivatives, e.g.
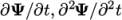
- gradSchemes: gradient
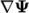
- divSchemes: divergence

- laplacianSchemes: Laplacian
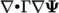 , with
diffusivity
, with
diffusivity 
- interpolationSchemes: cell to face interpolations of values.
- snGradSchemes: component of gradient normal to a cell face.
- wallDist: distance to wall calculation, where required.
Each keyword is the name of a sub-dictionary
which contains terms of a particular type, e.g. gradSchemes contains all the gradient
derivative terms such as grad(p) (which represents 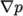 ). Further examples
can be seen in the extract from an fvSchemes dictionary below:
). Further examples
can be seen in the extract from an fvSchemes dictionary below:
17ddtSchemes
18{
19 default Euler;
20}
21
22gradSchemes
23{
24 default Gauss linear;
25}
26
27divSchemes
28{
29 default none;
30
31 div(phi,U) Gauss linearUpwind grad(U);
32 div(phi,k) Gauss upwind;
33 div(phi,epsilon) Gauss upwind;
34 div(phi,R) Gauss upwind;
35 div(R) Gauss linear;
36 div(phi,nuTilda) Gauss upwind;
37
38 div((nuEff*dev2(T(grad(U))))) Gauss linear;
39}
40
41laplacianSchemes
42{
43 default Gauss linear corrected;
44}
45
46interpolationSchemes
47{
48 default linear;
49}
50
51snGradSchemes
52{
53 default corrected;
54}
55
56
57// ************************************************************************* //
The example shows fvSchemes with 6 …Schemes subdictionaries, each containing
keyword entries including: a default entry; other entries for the
particular term specified, e.g.
div(phi, k) for 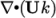 . If a default scheme is specified in a particular
…Schemes sub-dictionary, it is
assigned to all of the terms to which the sub-dictionary refers,
e.g. specifying a default in gradSchemes sets the scheme for all
gradient terms in the application, e.g.
. If a default scheme is specified in a particular
…Schemes sub-dictionary, it is
assigned to all of the terms to which the sub-dictionary refers,
e.g. specifying a default in gradSchemes sets the scheme for all
gradient terms in the application, e.g. 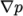 ,
,  . With a default specified, the specific terms are not
required in that sub-dictionary, i.e. the entries for grad(p), grad(U) are omitted in this example.
Specifying a particular will however override the default scheme.
. With a default specified, the specific terms are not
required in that sub-dictionary, i.e. the entries for grad(p), grad(U) are omitted in this example.
Specifying a particular will however override the default scheme.
The user can specify no default scheme by the none entry, as in the divSchemes in the example above. The user is then obliged to specify all terms in that sub-dictionary individually. Setting default to none ensures the user specifies all terms individually which is common for divSchemes which requires precise configuration.
OpenFOAM includes a vast number of discretisation schemes, from which only a few are typically recommended for real-world, engineering applications. The user can get help with scheme selection by interrogating the tutorial cases for example scheme settings. They should look at the schemes used in relevant cases, e.g. for running a large-eddy simulation (LES), look at schemes used in tutorials running LES. Additionally, foamSearch is a useful tool to list the schemes used in all the tutorials. For example, to print all the default entries for ddtSchemes for cases in the $FOAM_TUTORIALS directory, the user can type:
foamSearch $FOAM_TUTORIALS fvSchemes ddtSchemes/default
default backward;
default CrankNicolson 0.9;
default Euler;
default localEuler;
default none;
default steadyState;
4.5.1 Time schemes
The first time derivative (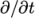 ) terms are specified in
the ddtSchemes sub-dictionary.
The discretisation schemes for each term can be selected from those
listed below.
) terms are specified in
the ddtSchemes sub-dictionary.
The discretisation schemes for each term can be selected from those
listed below.
- steadyState: sets time derivatives to zero.
- Euler: transient, first order implicit, bounded.
- backward: transient, second order implicit, potentially unbounded.
- CrankNicolson: transient, second order implicit, bounded;
requires an off-centering coefficient
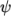 where:
where:
generally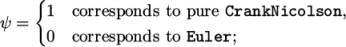
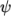 = 0.9 is used to stabilise the scheme for practical
engineering problems.
= 0.9 is used to stabilise the scheme for practical
engineering problems. - localEuler: pseudo transient for accelerating a solution to steady-state using local-time stepping; first order implicit.
Any second time derivative ( ) terms are specified in
the d2dt2Schemes
sub-dictionary. Only the Euler
scheme is available for d2dt2Schemes.
) terms are specified in
the d2dt2Schemes
sub-dictionary. Only the Euler
scheme is available for d2dt2Schemes.
4.5.2 Gradient schemes
The gradSchemes sub-dictionary contains gradient terms. The default discretisation scheme that is primarily used for gradient terms is:
default Gauss linear;
In some tutorials cases, particular involving poorer quality meshes, the discretisation of specific gradient terms is then overridden to improve boundedness and stability. The terms that are overridden in those cases are the velocity gradient
grad(U) cellLimited Gauss linear 1;
grad(k) cellLimited Gauss linear 1;
grad(epsilon) cellLimited Gauss linear 1;
Other schemes that are rarely used are as follows.
- leastSquares: a second-order, least squares distance calculation using all neighbour cells.
- Gauss cubic: third-order scheme that appears in solidDisplacement and dnsFoam examples.
4.5.3 Divergence schemes
The divSchemes sub-dictionary contains
divergence terms, i.e. terms of the form  …, excluding
Laplacian terms (of the form
…, excluding
Laplacian terms (of the form 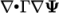 ). This includes both
advection terms, e.g.
). This includes both
advection terms, e.g. 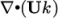 , where velocity
, where velocity
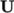 provides the advective flux, and other terms, that are often
diffusive in nature, e.g.
provides the advective flux, and other terms, that are often
diffusive in nature, e.g. 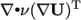 .
.
The fact that terms that are fundamentally different reside in one sub-dictionary means that the default scheme in generally set to none in divSchemes. The non-advective terms then generally use the Gauss integration with linear interpolation, e.g.
div(U) Gauss linear;
The treatment of advective terms is one of the major challenges in CFD numerics and so the options are more extensive. The keyword identifier for the advective terms are usually of the form div(phi,…), where phi denotes the (volumetric) flux of velocity on the cell faces for constant-density flows and the mass flux for compressible flows, e.g. div(phi,U) for the advection of velocity, div(phi,e) for the advection of internal energy, etc. For advection of velocity, the user can run the foamSearch script to extract the div(phi,U) keyword from all tutorials.
foamSearch $FOAM_TUTORIALS fvSchemes "divSchemes/div(phi,U)"
Ignoring ‘V’-schemes (with keywords ending “V”), and rarely-used schemes such as Gauss cubic and vanLeerV, the interpolation schemes used in the tutorials are as follows.
- linear: second order, unbounded.
- linearUpwind: second order, upwind-biased, unbounded (but much less so than linear), that requires discretisation of the velocity gradient to be specified.
- LUST: blended 75% linear/ 25%linearUpwind scheme, that requires discretisation of the velocity gradient to be specified.
- limitedLinear: linear scheme that limits towards upwind in regions of rapidly changing gradient; requires a coefficient, where 1 is strongest limiting, tending towards linear as the coefficient tends to 0.
- upwind: first-order bounded, generally too inaccurate for velocity but more often used for transport of scalar fields.
Example syntax for these schemes is as follows.
div(phi,U) Gauss linear;
div(phi,U) Gauss linearUpwind grad(U);
div(phi,U) Gauss LUST grad(U);
div(phi,U) Gauss LUST unlimitedGrad(U);
div(phi,U) Gauss limitedLinear 1;
div(phi,U) Gauss upwind;
‘V’-schemes are specialised versions of schemes designed for vector fields. They differ from conventional schemes by calculating a single limiter which is applied to all components of the vectors, rather than calculating separate limiters for each component of the vector. The ‘V’-schemes’ single limiter is calculated based on the direction of most rapidly changing gradient, resulting in the strongest limiter being calculated which is most stable but arguably less accurate. Example syntax is as follows.
div(phi,U) Gauss limitedLinearV 1;
div(phi,U) Gauss linearUpwindV grad(U);
The bounded variants of schemes relate to the treatment of
the material time derivative which can be expressed in terms of a
spatial time derivative and convection, e.g. for field  in incompressible
flow
in incompressible
flow
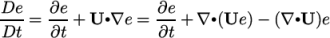 |
(4.1) |
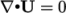 at convergence, at
which point the third term on the right hand side is zero. Before
convergence is reached, however,
at convergence, at
which point the third term on the right hand side is zero. Before
convergence is reached, however,  and in some
circumstances, particularly steady-state simulations, it is better
to include the third term within a numerical solution to help
maintain boundedness of the solution variable and promote better
convergence. The bounded variant of the
Gauss scheme provides this,
automatically including the discretisation of the third-term with
the advection term. Example syntax is as follows, as seen in
fvSchemes files for
steady-state cases.
and in some
circumstances, particularly steady-state simulations, it is better
to include the third term within a numerical solution to help
maintain boundedness of the solution variable and promote better
convergence. The bounded variant of the
Gauss scheme provides this,
automatically including the discretisation of the third-term with
the advection term. Example syntax is as follows, as seen in
fvSchemes files for
steady-state cases.
div(phi,U) bounded Gauss limitedLinearV 1;
div(phi,U) bounded Gauss linearUpwindV grad(U);
The schemes used for advection of scalar fields are similar to those for advection of velocity, although in general there is greater emphasis placed on boundedness than accuracy when selecting the schemes. For example, a search for schemes for advection of internal energy (e) reveals the following.
foamSearch $FOAM_TUTORIALS fvSchemes "divSchemes/div(phi,e)"
div(phi,e) bounded Gauss upwind;
div(phi,e) Gauss limitedLinear 1;
div(phi,e) Gauss linearUpwind limited;
div(phi,e) Gauss LUST grad(e);
div(phi,e) Gauss upwind;
div(phi,e) Gauss vanAlbada;
There are specialised versions of the limited
schemes for scalar fields that are commonly bounded between 0 and 1,
e.g. the laminar flame
speed regress variable  . A search for the discretisation used for
advection in the laminar flame transport equation yields:
. A search for the discretisation used for
advection in the laminar flame transport equation yields:
div(phiSt,b) Gauss limitedLinear01 1;
The multivariateSelection mechanism also exists
for grouping multiple equation terms together, and applying the
same limiters on all terms, using the strongest limiter calculated
for all terms. A good example of this is in a set of mass transport
equations for fluid species, where it is good practice to apply the
same discretisation to all equations for consistency. The example
below comes from the smallPoolFire3D tutorial in $FOAM_TUTORIALS/multicompon/entFluid, in which
the equation for enthalpy  is included with the specie mass transport
equations in the calculation of a single limiter.
is included with the specie mass transport
equations in the calculation of a single limiter.
div(phi,Yi_h) Gauss multivariateSelection
{
O2 limitedLinear01 1;
CH4 limitedLinear01 1;
N2 limitedLinear01 1;
H2O limitedLinear01 1;
CO2 limitedLinear01 1;
h limitedLinear 1 ;
}
4.5.4 Surface normal gradient schemes
It is worth explaining the snGradSchemes sub-dictionary that contains surface normal gradient terms, before discussion of laplacianSchemes, because they are required to evaluate a Laplacian term using Gaussian integration. A surface normal gradient is evaluated at a cell face; it is the component, normal to the face, of the gradient of values at the centres of the 2 cells that the face connects.
A search for the default scheme for snGradSchemes reveals the following entries.
default corrected;
default limited corrected 0.33;
default limited corrected 0.5;
default orthogonal;
default uncorrected;
The basis of the gradient calculation at a face is to subtract the value at the cell centre on one side of the face from the value in the centre on the other side and divide by the distance. The calculation is second-order accurate for the gradient normal to the face if the vector connecting the cell centres is orthogonal to the face, i.e. they are at right-angles. This is the orthogonal scheme.
Orthogonality requires a regular mesh, typically
aligned with the Cartesian co-ordinate system, which does not
generally occur with real world, engineering geometries. Therefore,
to maintain second-order accuracy, an explicit non-orthogonal
correction can be added to the orthogonal component, known as the
corrected scheme. The correction
increases in size as the non-orthogonality, i.e. the angle 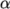 between the cell-cell
vector and face normal vector, increases.
between the cell-cell
vector and face normal vector, increases.
As 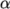 tends towards
tends towards 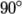 , typically beyond
, typically beyond
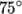 ,
the explicit correction can be so large to cause a solution to go
unstable. The solution can be stabilised by applying the
limited scheme to the correction
which requires a coefficient
,
the explicit correction can be so large to cause a solution to go
unstable. The solution can be stabilised by applying the
limited scheme to the correction
which requires a coefficient 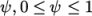 where
where
 |
(4.2) |
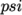 is chosen to be 0.33 or 0.5, where 0.33 offers greater
stability and 0.5 greater accuracy.
is chosen to be 0.33 or 0.5, where 0.33 offers greater
stability and 0.5 greater accuracy.
The corrected scheme applies under-relaxation in
which the implicit orthogonal calculation is increased by
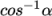 ,
with an equivalent boost within the non-orthogonal correction. The
uncorrected scheme is equivalent to
the corrected scheme, without the
non-orthogonal correction, so is like orthogonal but with the additional
,
with an equivalent boost within the non-orthogonal correction. The
uncorrected scheme is equivalent to
the corrected scheme, without the
non-orthogonal correction, so is like orthogonal but with the additional
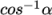 under-relaxation.
under-relaxation.
Generally the uncorrected and orthogonal schemes are only recommended for
meshes with very low non-orthogonality (e.g. maximum 5 ). The corrected scheme is generally recommended,
but for maximum non-orthogonality above 75
). The corrected scheme is generally recommended,
but for maximum non-orthogonality above 75 , limited may be required. At
non-orthogonality above 85
, limited may be required. At
non-orthogonality above 85 , convergence is generally hard to achieve.
, convergence is generally hard to achieve.
4.5.5 Laplacian schemes
The laplacianSchemes sub-dictionary contains
Laplacian terms. A typical Laplacian term is  , the diffusion term in
the momentum equations, which corresponds to the keyword
laplacian(nu,U) in laplacianSchemes. The Gauss scheme is the only choice of
discretisation and requires a selection of both an interpolation
scheme for the diffusion coefficient, i.e.
, the diffusion term in
the momentum equations, which corresponds to the keyword
laplacian(nu,U) in laplacianSchemes. The Gauss scheme is the only choice of
discretisation and requires a selection of both an interpolation
scheme for the diffusion coefficient, i.e.  in our example, and a
surface normal gradient scheme, i.e.
in our example, and a
surface normal gradient scheme, i.e.  . To summarise, the
entries required are:
. To summarise, the
entries required are:
Gauss <interpolationScheme> <snGradScheme>
foamSearch $FOAM_TUTORIALS fvSchemes laplacianSchemes/default
default Gauss linear corrected;
default Gauss linear limited corrected 0.33;
default Gauss linear limited corrected 0.5;
default Gauss linear orthogonal;
default Gauss linear uncorrected;
4.5.6 Interpolation schemes
The interpolationSchemes sub-dictionary contains terms that are interpolations of values typically from cell centres to face centres, primarily used in the interpolation of velocity to face centres for the calculation of flux phi. There are numerous interpolation schemes in OpenFOAM, but a search for the default scheme in all the tutorial cases reveals that linear interpolation is used in almost every case, except for one stress analysis example which uses cubic interpolation.

