[version 13][version 12][version 11][version 10][version 9][version 8][version 7][version 6]
4.6 Solution and algorithm control
Once a matrix equation is constructed according to the schemes in the previous section, a linear solver is applied. A set of equations is also framed within an algorithm containing loops and controls. For information about the main algorithms and solvers in OpenFOAM, refer to Chapter 5 of Notes on Computational Fluid Dynamics: General Principles.
The controls for algorithms and solvers are found in the fvSolution dictionary in the system directory. Below is an example set of entries from the fvSolution dictionary for a case using the incompressibleFluid modular solver.
17solvers
18{
19 p
20 {
21 solver GAMG;
22 tolerance 1e-7;
23 relTol 0.01;
24
25 smoother DICGaussSeidel;
26
27 }
28
29 pFinal
30 {
31 $p;
32 relTol 0;
33 }
34
35 "(U|k|epsilon)"
36 {
37 solver smoothSolver;
38 smoother symGaussSeidel;
39 tolerance 1e-05;
40 relTol 0.1;
41 }
42
43 "(U|k|epsilon)Final"
44 {
45 $U;
46 relTol 0;
47 }
48}
49
50PIMPLE
51{
52 nNonOrthogonalCorrectors 0;
53 nCorrectors 2;
54}
55
56
57// ************************************************************************* //
fvSolution contains a set of subdictionaries, described in the remainder of this section that includes: solvers; relaxationFactors; and, SIMPLE for steady-state cases or PIMPLE for transient or pseudo-transient cases.
4.6.1 Linear solver control
The first sub-dictionary in our example is solvers. It specifies each linear solver that is used for each discretised equation; here, the term linear solver refers to the method of number-crunching to solve a matrix equation, as opposed to an modular solver, such as incompressibleFluid which describes the entire set of equations and algorithms to solve a particular problem. The term ‘linear solver’ is abbreviated to ‘solver’ in much of what follows; hopefully the context of the term avoids any ambiguity.
The syntax for each entry within solvers starts with a keyword that for the
variable being solved in the particular equation. For example,
incompressibleFluid solves
equations for pressure 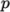 , velocity
, velocity 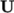 and often turbulence
fields, hence the entries for p,
U, k and epsilon. The keyword introduces a
sub-dictionary containing the type of solver and the parameters
that the solver uses. The solver is selected through the
solver keyword from the options
listed below. The parameters, including tolerance, relTol, preconditioner, etc. are described in following
sections.
and often turbulence
fields, hence the entries for p,
U, k and epsilon. The keyword introduces a
sub-dictionary containing the type of solver and the parameters
that the solver uses. The solver is selected through the
solver keyword from the options
listed below. The parameters, including tolerance, relTol, preconditioner, etc. are described in following
sections.
- PCG/PBiCGStab: Stabilised preconditioned (bi-)conjugate gradient, for both symmetric and asymmetric matrices.
- PCG/PBiCG: preconditioned (bi-)conjugate gradient, with PCG for symmetric matrices, PBiCG for asymmetric matrices.
- smoothSolver: solver that uses a smoother.
- GAMG: generalised geometric-algebraic multi-grid.
- diagonal: diagonal solver for explicit systems.
The solvers distinguish between symmetric matrices and asymmetric matrices. The symmetry of the matrix depends on the terms of the equation being solved, e.g. time derivatives and Laplacian terms form coefficients of a symmetric matrix, whereas an advective derivative introduces asymmetry. If the user specifies a symmetric solver for an asymmetric matrix, or vice versa, an error message will be written to advise the user accordingly, e.g.
--> FOAM FATAL IO ERROR : Unknown asymmetric matrix solver PCG
Valid asymmetric matrix solvers are :
4
(
GAMG
PBiCG
PBiCGStab
smoothSolver
)
4.6.2 Solution tolerances
The finite volume method generally solves equations in a segregated, decoupled manner, meaning that each matrix equation solves for only one variable. The matrices are consequently sparse, meaning they predominately include coefficients of 0. The solvers are generally iterative, i.e. they are based on reducing the equation residual over successive solutions. The residual is ostensibly a measure of the error in the solution so that the smaller it is, the more accurate the solution. More precisely, the residual is evaluated by substituting the current solution into the equation and taking the magnitude of the difference between the left and right hand sides; it is also normalised to make it independent of the scale of the problem being analysed.
Before solving an equation for a particular field, the initial residual is evaluated based on the current values of the field. After each solver iteration the residual is re-evaluated. The solver stops if any one of the following conditions are reached:
- the residual falls below the solver tolerance, tolerance;
- the ratio of current to initial residuals falls below the solver relative tolerance, relTol;
- the number of iterations exceeds a maximum number of iterations, maxIter;
The solver tolerance should represent the level at which the residual is small enough that the solution can be deemed sufficiently accurate. The solver relative tolerance limits the relative improvement from initial to final solution. In transient simulations, it is usual to set the solver relative tolerance to 0 to force the solution to converge to the solver tolerance in each time step. The tolerances, tolerance and relTol must be specified in the dictionaries for all solvers; maxIter is optional and defaults to a value of 1000.
Equations are very often solved multiple times within one solution step, or time step. For example, when using the PIMPLE algorithm, a pressure equation is solved according to the number specified by nCorrectors, as described in section 4.6.7 . Where this occurs, the solver is very often set up to use different settings when solving the particular equation for the final time, specified by a keyword that adds Final to the field name. For example, in the transient pitzDaily example for the incompressibleFluid solver, the solver settings for pressure are as follows.
p
{
solver GAMG;
tolerance 1e-07;
relTol 0.01;
smoother DICGaussSeidel;
}
pFinal
{
$p;
relTol 0;
}
4.6.3 Preconditioned conjugate gradient solvers
There are a range of options for preconditioning of matrices in the conjugate gradient solvers, represented by the preconditioner keyword in the solver dictionary, listed below. Note that the DIC/DILU preconditioners are exclusively specified in the tutorials in OpenFOAM.
- DIC/DILU: diagonal incomplete-Cholesky (symmetric) and incomplete-LU (asymmetric)
- FDIC: slightly faster diagonal incomplete-Cholesky (DIC with caching, symmetric)
- GAMG: geometric-algebraic multi-grid.
- diagonal: diagonal preconditioning, not generally used.
- none: no preconditioning.
4.6.4 Smooth solvers
The solvers that use a smoother require the choice of smoother to be specified. The smoother options are listed below. The symGaussSeidel and GaussSeidel smoothers are preferred in the tutorials.
- GaussSeidel: Gauss-Seidel.
- symGaussSeidel: symmetric Gauss-Seidel.
- DIC/DILU: diagonal incomplete-Cholesky (symmetric), incomplete-LU (asymmetric).
- DICGaussSeidel: diagonal incomplete-Cholesky/LU with Gauss-Seidel (symmetric/asymmetric).
When using the smooth solvers, the user can optionally specify the number of sweeps, by the nSweeps keyword, before the residual is recalculated. Without setting it, it reverts to a default value of 1.
4.6.5 Geometric-algebraic multi-grid solvers
The geometric-algebraic multi-grid (GAMG) method uses the principle of: generating a quick solution on a mesh with a small number of cells; mapping this solution onto a finer mesh; using it as an initial guess to obtain an accurate solution on the fine mesh. GAMG is faster than standard methods when the increase in speed by solving first on coarser meshes outweighs the additional costs of mesh refinement and mapping of field data. In practice, GAMG starts with the original mesh and coarsens/refines the mesh in stages. The coarsening is limited by a specified minimum number of cells at the most coarse level.
The agglomeration of cells is performed by the method specified by the agglomerator keyword. The tutorials all use the default faceAreaPair method. The agglomeration can be controlled using the following optional entries, most of which default in the tutorials.
- cacheAgglomeration: switch specifying caching of the agglomeration strategy (default true).
- nCellsInCoarsestLevel: approximate mesh size at the most coarse level in terms of the number of cells (default 10).
- directSolveCoarset: use a direct solver at the coarsest level (default false).
- mergeLevels: keyword controls the speed at which coarsening or refinement is performed; the default is 1, which is safest, but for simple meshes, the solution speed can be increased by coarsening/refining 2 levels at a time, i.e. setting mergeLevels 2.
Smoothing is specified by the smoother as described in section 4.6.4. The number of sweeps used by the smoother at different levels of mesh density are specified by the following optional entries.
- nPreSweeps: number of sweeps as the algorithm is coarsening (default 0).
- preSweepsLevelMultiplier: multiplier for the number of sweeps between each coarsening level (default 1).
- maxPreSweeps: maximum number of sweeps as the algorithm is coarsening (default 4).
- nPostSweeps: number of sweeps as the algorithm is refining (default 2).
- postSweepsLevelMultiplier: multiplier for the number of sweeps between each refinement level (default 1).
- maxPostSweeps: maximum number of sweeps as the algorithm is refining (default 4).
- nFinestSweeps: number of sweeps at finest level (default 2).
4.6.6 Solution under-relaxation
The fvSolution file usually includes a
relaxationFactors
sub-dictionary which controls under-relaxation. Under-relaxation is
used to improve stability of a computation, particularly for
steady-state problems. It works by limiting the amount which a
variable changes from one iteration to the next, either by
manipulating the matrix equation prior to solving for a field, or by
modifying the field afterwards. An under-relaxation factor
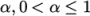 specifies the amount of under-relaxation, as described below.
specifies the amount of under-relaxation, as described below.
- No specified
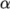 : no
under-relaxation.
: no
under-relaxation. 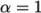 : guaranteed matrix diagonal
equality/dominance.
: guaranteed matrix diagonal
equality/dominance.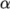 decreases, under-relaxation increases.
decreases, under-relaxation increases.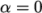 : solution does not change with successive
iterations.
: solution does not change with successive
iterations.
An optimum choice of 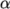 is one that is small
enough to ensure stable computation but large enough to move the
iterative process forward quickly; values of
is one that is small
enough to ensure stable computation but large enough to move the
iterative process forward quickly; values of 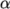 as high as 0.9 can
ensure stability in some cases and anything much below, say, 0.2
can be prohibitively restrictive in slowing the iterative process.
as high as 0.9 can
ensure stability in some cases and anything much below, say, 0.2
can be prohibitively restrictive in slowing the iterative process.
Relaxation factors for under-relaxation of fields are specified within a field sub-dictionary; relaxation factors for equation under-relaxation are within a equations sub-dictionary. An example is shown below from a case with the incompressibleFluid solver module running in steady-state mode. The factors are specified for pressure p, pressure U, and turbulent fields grouped using a regular expression.
55{
56 fields
57 {
58 p 0.3;
59 }
60 equations
61 {
62 U 0.7;
63 "(k|omega|epsilon).*" 0.7;
64 }
65}
66
67// ************************************************************************* //
For a transient case with the incompressibleFluid module, under-relaxation would simply slow convergence of the solution within each time step. Instead, the following setting is generally adopted to ensure diagonal equality which is generally required for convergence of a matrix equation.
61{
62 equations
63 {
64 ".*" 1;
65 }
66}
67
68
69// ************************************************************************* //
4.6.7 SIMPLE and PIMPLE algorithms
Most fluid solver modules use algorithms to couple equations for mass and momentum conservation known as:
- SIMPLE (semi-implicit method for pressure-linked equations);
- PIMPLE, a combination of PISO (pressure-implicit split-operator) and SIMPLE.
Within in time, or solution, step, the algorithms solve a pressure equation, to enforce mass conservation, with an explicit correction to velocity to satisfy momentum conservation. They optionally begin each step by solving the momentum equation — the so-called momentum predictor.
While all the algorithms solve the same governing equations (albeit in different forms), the algorithms principally differ in how they loop over the equations. The looping is controlled by input parameters that are listed below. They are set in a dictionary named after the algorithm, i.e. SIMPLE, or PIMPLE.
- nCorrectors: used by PIMPLE, sets the number of times the algorithm solves the pressure equation and momentum corrector in each step; typically set to 2 or 3.
- nNonOrthogonalCorrectors: used by all algorithms,
specifies repeated solutions of the pressure equation, used to
update the explicit non-orthogonal correction, described in
section 4.5.4
, of the Laplacian term
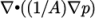 ;
typically set to 0 for steady-state and 1 for transient cases.
;
typically set to 0 for steady-state and 1 for transient cases. - nOuterCorrectors: used by PIMPLE, it
enables looping over the entire system of equations within on time
step, representing the total number of times the system is solved;
must be
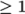 and is typically set to 1.
and is typically set to 1. - momentumPredictor: switch that controls solving of the momentum predictor; typically set to off for some flows, including low Reynolds number and multiphase.
4.6.8 Pressure referencing
In a closed incompressible system, pressure is relative: it is the pressure range that matters not the absolute values. In these cases, the solver sets a reference level of pRefValue in cell pRefCell. These entries are generally stored in the SIMPLE or PIMPLE sub-dictionary.

