[version 13][version 12][version 11][version 10][version 9][version 8][version 7][version 6]
Chapter 7 Models and physical properties
OpenFOAM includes a large range of solvers, each designed for a specific class of flow, as described in section 3.5 . Each solver uses a particular set of models which calculate physical properties and simulate phenomena like transport, turbulence, thermal radiation, etc.
From OpenFOAM v10 onwards, a distinction is made
between material properties and
models for phenomena such as those mentioned above. Properties are specified in physicalProperties file in the constant directory. In the case of fluids, properties
in physicalProperties relate
to a fluid at rest. They are the properties you might look up from a
table in a book, so can be dependent on temperature 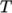 , based on some
function.
, based on some
function.
Properties described in physicalProperties do not include any
dependency on the flow itself. For example, turbulence,
visco-elasticity and the variation of viscosity  with strain-rate,
are all specified in a momentumTransport file in the constant directory. This chapter includes
a description of models for viscosity which are dependent on
strain-rate in section 7.3
and turbulence models
in section 7.2
. Thermophysical
models, which are specified in the physicalProperties file (since they
represent temperature dependency of properties) are described in
section 7.1
.
with strain-rate,
are all specified in a momentumTransport file in the constant directory. This chapter includes
a description of models for viscosity which are dependent on
strain-rate in section 7.3
and turbulence models
in section 7.2
. Thermophysical
models, which are specified in the physicalProperties file (since they
represent temperature dependency of properties) are described in
section 7.1
.
7.1.1 Thermophysical and mixture models
7.1.2 Transport model
7.1.3 Thermodynamic models
7.1.4 Composition of each constituent
7.1.5 Equation of state
7.1.6 Selection of energy variable
7.1.7 Thermophysical property data
7.2 Turbulence models
7.2.1 Reynolds-averaged simulation (RAS) modelling
7.2.2 Large eddy simulation (LES) modelling
7.2.3 Model coefficients
7.2.4 Wall functions
7.3 Transport/rheology models
7.3.1 Bird-Carreau model
7.3.2 Cross Power Law model
7.3.3 Power Law model
7.3.4 Herschel-Bulkley model
7.3.5 Casson model
7.3.6 General strain-rate function
7.3.7 Maxwell model
7.3.8 Giesekus model
7.3.9 Phan-Thien-Tanner (PTT) model
7.3.10 Lambda thixotropic model

