8.5 Unstructured hex-dominant meshes
While block-structured meshes are effective for model problems with simple boundaries, e.g. a cylinder, they are impractical for many engineering applications, e.g. automotive aerodynamics.
Instead, CFD practitioners turn to tools which can generate meshes of many millions of cells and accommodate complex boundaries, e.g. a from a CAD model of a vehicle, in a highly automated manner.
A logical approach is to apply hexahedral-shaped cells that are oriented with the known, or anticipated, direction of flow. This is possible towards far-field boundaries and along solid walls, with the far-field cells generally larger than those at solid walls.

Cells must then be generated to fill the region between the aligned meshes near the far-field and solid boundaries. One approach is to infill the region with tetrahedral-shaped cells using automated methods based on Delaunay triangulation.2
A more recent strategy is to fill the entire domain with large cells, similar to those in the far-field, which are then progressively split until they reach the desired size at solid boundaries. Subsequent steps then conform and align the cells to the solid boundaries.
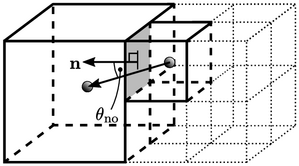
The infill region then contains mainly hexahedra, with the mesh described as “hex-dominant”. Where there is transition in levels of cell splitting (see above), the larger cells become polyhedrons with an increased number of faces due to the smaller cells.
The splitting reduces solution accuracy by
introducing a modest amount of non-orthogonality at the
intersecting faces, i.e.
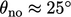 for cells of unit aspect ratio. It also causes the weights
for cells of unit aspect ratio. It also causes the weights
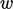 for interpolation schemes, see Sec. 3.7
, to deviate
from the ideal
for interpolation schemes, see Sec. 3.7
, to deviate
from the ideal 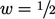 ; instead, for cells of unit aspect ratio,
; instead, for cells of unit aspect ratio,
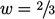 (or
(or  ).
).

The generation of unstructured hex-dominant meshes is highly automatable, using simple controls that define the levels of cell splitting within specified regions of the domain, as shown above.

