[version 13][version 12][version 11][version 10][version 9][version 8][version 7][version 6]
7.3 Transport/rheology models
In OpenFOAM, solvers that do not include
energy/heat, include a library of models for viscosity  . The models
typically relate viscosity to strain rate
. The models
typically relate viscosity to strain rate 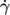 and are specified by the
user in the transportProperties dictionary. The
available models are listed in the following sections.
and are specified by the
user in the transportProperties dictionary. The
available models are listed in the following sections.
7.3.1 Newtonian model
The Newtonian model
assumes  is constant. Viscosity is specified by a dimensionedScalar nu in transportProperties, e.g.
is constant. Viscosity is specified by a dimensionedScalar nu in transportProperties, e.g.
transportModel Newtonian;
nu [ 0 2 -1 0 0 0 0 ] 1.5e-05;
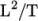 .
.
7.3.2 Bird-Carreau model
![a(n−1)∕a ν = ν∞ + (ν0 − ν∞)[1 + (k ˙γ) ] \relax \special {t4ht=](img/index555x.png) |
(7.21) |
 has a default value of 2. An example
specification of the model in transportProperties is:
has a default value of 2. An example
specification of the model in transportProperties is:
transportModel BirdCarreau;
BirdCarreauCoeffs
{
nu0 [ 0 2 -1 0 0 0 0 ] 1e-03;
nuInf [ 0 2 -1 0 0 0 0 ] 1e-05;
k [ 0 0 1 0 0 0 0 ] 1;
n [ 0 0 0 0 0 0 0 ] 0.5;
}
7.3.3 Cross Power Law model
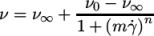 |
(7.22) |
transportModel CrossPowerLaw;
CrossPowerLawCoeffs
{
nu0 [ 0 2 -1 0 0 0 0 ] 1e-03;
nuInf [ 0 2 -1 0 0 0 0 ] 1e-05;
m [ 0 0 1 0 0 0 0 ] 1;
n [ 0 0 0 0 0 0 0 ] 0.5;
}
7.3.4 Power Law model
The Power Law model
provides a function for viscosity, limited by minimum and maximum
values,  and
and 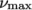 respectively. The function is:
respectively. The function is:
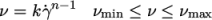 |
(7.23) |
transportModel powerLaw;
powerLawCoeffs
{
nuMax [ 0 2 -1 0 0 0 0 ] 1e-03;
nuMin [ 0 2 -1 0 0 0 0 ] 1e-05;
k [ 0 2 -1 0 0 0 0 ] 1e-05;
n [ 0 0 0 0 0 0 0 ] 1;
}
7.3.5 Herschel-Bulkley model
The
Herschel-Bulkley model combines the effects of Bingham plastic and
power-law behavior in a fluid. For low strain rates, the material is
modelled as a very viscous fluid with viscosity 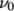 . Beyond a threshold in
strain-rate corresponding to threshold stress
. Beyond a threshold in
strain-rate corresponding to threshold stress 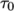 , the viscosity is
described by a power law. The model is:
, the viscosity is
described by a power law. The model is:
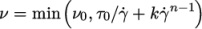 |
(7.24) |
transportModel HerschelBulkley;
HerschelBulkleyCoeffs
{
nu0 [ 0 2 -1 0 0 0 0 ] 1e-03;
tau0 [ 0 2 -2 0 0 0 0 ] 1;
k [ 0 2 -1 0 0 0 0 ] 1e-05;
n [ 0 0 0 0 0 0 0 ] 1;
}
7.3.6 Casson model
The Casson model is a basic
model used in blood rheology that specifies minimum and maximum
viscosities,  and
and 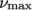 respectively. Beyond a threshold in strain-rate
corresponding to threshold stress
respectively. Beyond a threshold in strain-rate
corresponding to threshold stress 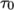 , the viscosity is
described by a “square-root” relationship. The model is:
, the viscosity is
described by a “square-root” relationship. The model is:
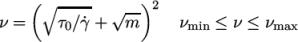 |
(7.25) |
transportModel Casson;
CassonCoeffs
{
m [ 0 2 -1 0 0 0 0 ] 3.934986e-6;
tau0 [ 0 2 -2 0 0 0 0 ] 2.9032e-6;
nuMax [ 0 2 -1 0 0 0 0 ] 13.3333e-6;
nuMin [ 0 2 -1 0 0 0 0 ] 3.9047e-6;
}
7.3.7 General strain-rate function
A strainRateFunction model exists that allows a user to specify viscosity as a function of strain rate at run-time. It uses the same Function1 functionality to specify the function of strain-rate, used by time varying properties in boundary conditions described in section 5.2.3.4 . An example specification of the model in transportProperties is shown below using the polynomial function:
transportModel strainRateFunction;
strainRateFunctionCoeffs
{
function polynomial ((0 0.1) (1 1.3));
}

