[version 13][version 12][version 11][version 10][version 9][version 8][version 7][version 6]
7.3 Transport/rheology models
In OpenFOAM, simulations that include flow
without energy/heat require modelling of the fluid stress. Many
simulations assume a Newtonian
fluid in which a viscosity
 is
specified in physicalProperties, e.g. by
is
specified in physicalProperties, e.g. by
viscosityModel constant;
nu 1.5e-05;
- a family of generalisedNewtonian models for a non-uniform
viscosity which is a function of strain rate
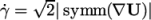 , described in
sections 7.3.1
, 7.3.2,
7.3.3
, 7.3.4
, 7.3.5 and
7.3.6
;
, described in
sections 7.3.1
, 7.3.2,
7.3.3
, 7.3.4
, 7.3.5 and
7.3.6
; - a set of visco-elastic models, including Maxwell, Giesekus and PTT (Phan-Thien & Tanner), described in sections 7.3.7 , 7.3.8 and 7.3.9 , respectively;
- the lambdaThixotropic model, described in section 7.3.10 .
7.3.1 Bird-Carreau model
The Bird-Carreau generalisedNewtonian model is
![a(n−1)∕a ν = ν∞ + (ν0 − ν∞)[1 + (k ˙γ) ] \relax \special {t4ht=](img/index555x.png) |
(7.22) |
 has a default value of 2. An example
specification of the model in momentumTransport is:
has a default value of 2. An example
specification of the model in momentumTransport is:
viscosityModel BirdCarreau;
nuInf 1e-05;
k 1;
n 0.5;
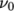 , is specified in
the physicalProperties file.
, is specified in
the physicalProperties file.
7.3.2 Cross Power Law model
The Cross Power Law generalisedNewtonian model is:
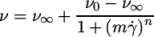 |
(7.23) |
viscosityModel CrossPowerLaw;
nuInf 1e-05;
m 1;
n 0.5;
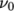 , is specified in
the physicalProperties file.
, is specified in
the physicalProperties file.
7.3.3 Power Law model
The Power Law
generalisedNewtonian model provides a
function for viscosity, limited by minimum and maximum values,
 and
and
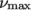 respectively. The function is:
respectively. The function is:
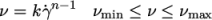 |
(7.24) |
viscosityModel powerLaw;
nuMax 1e-03;
nuMin 1e-05;
k 1e-05;
n 0.5;
7.3.4 Herschel-Bulkley model
The
Herschel-Bulkley generalisedNewtonian model combines the
effects of Bingham plastic and power-law behavior in a fluid. For low
strain rates, the material is modelled as a very viscous fluid with
viscosity 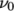 . Beyond a threshold in strain-rate corresponding to
threshold stress
. Beyond a threshold in strain-rate corresponding to
threshold stress 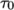 , the viscosity is described by a power law. The model
is:
, the viscosity is described by a power law. The model
is:
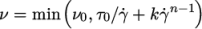 |
(7.25) |
viscosityModel HerschelBulkley;
tau0 0.01;
k 0.001;
n 0.5;
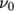 , is specified in
the physicalProperties file.
, is specified in
the physicalProperties file.
7.3.5 Casson model
The Casson generalisedNewtonian model is a basic model
used in blood rheology that specifies minimum and maximum
viscosities, 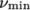 and
and 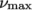 respectively. Beyond a threshold in strain-rate
corresponding to threshold stress
respectively. Beyond a threshold in strain-rate
corresponding to threshold stress 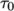 , the viscosity is
described by a “square-root” relationship. The model is:
, the viscosity is
described by a “square-root” relationship. The model is:
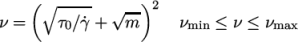 |
(7.26) |
viscosityModel Casson;
m 3.934986e-6;
tau0 2.9032e-6;
nuMax 13.3333e-6;
nuMin 3.9047e-6;
7.3.6 General strain-rate function
A strainRateFunction generalisedNewtonian model exists that allows a user to specify viscosity as a function of strain rate at run-time. It uses the same Function1 functionality to specify the function of strain-rate, used by time varying properties in boundary conditions described in section 5.2.3.4 . An example specification of the model in momentumTransport is shown below using the polynomial function:
viscosityModel strainRateFunction;
function polynomial ((0 0.1) (1 1.3));
7.3.7 Maxwell model
The Maxwell laminar visco-elastic model solves an
equation for the fluid stress tensor 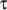 :
:
![∂-τ+ ∇ ∙(U τ) = 2 symm [τ∙∇U ]− 2νM-symm (∇U )− 1τ ∂t λ λ \relax \special {t4ht=](img/index572x.png) |
(7.27) |
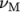 (nuM) is the “Maxwell”
viscosity and
(nuM) is the “Maxwell”
viscosity and 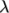 (lambda) is the
relaxation time. An example specification of model parameters is
shown below:
(lambda) is the
relaxation time. An example specification of model parameters is
shown below:
simulationType laminar;
laminar
{
model Maxwell;
MaxwellCoeffs
{
nuM 0.002;
lambda 0.03;
}
}
 , is
specified in the physicalProperties file, the model becomes
equivalent to an Oldroyd-B visco-elastic model. The Maxwell model
includes a multi-mode option where
, is
specified in the physicalProperties file, the model becomes
equivalent to an Oldroyd-B visco-elastic model. The Maxwell model
includes a multi-mode option where 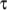 is a sum of stresses,
each with an associated relaxation time
is a sum of stresses,
each with an associated relaxation time 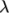 .
.
7.3.8 Giesekus model
The Giesekus laminar visco-elastic model is similar to
the Maxwell model but includes an additional “mobility” term in the
equation for 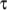 :
:
![∂ τ ν 1 α ---+ ∇ ∙(U τ) = 2 symm [τ∙∇U ]− 2-M- symm (∇U ) − -τ − -G-[τi∙τi] ∂t λ λ νM \relax \special {t4ht=](img/index579x.png) |
(7.28) |
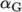 (alphaG) is the
mobility parameter. An example specification of model parameters is
shown below:
(alphaG) is the
mobility parameter. An example specification of model parameters is
shown below:
simulationType laminar;
laminar
{
model Giesekus;
GiesekusCoeffs
{
nuM 0.002;
lambda 0.03;
alphaG 0.1;
}
}
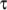 is a sum of
stresses, each with an associated relaxation time
is a sum of
stresses, each with an associated relaxation time 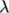 and mobility
coefficient
and mobility
coefficient 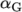 .
.
7.3.9 Phan-Thien-Tanner (PTT) model
The
Phan-Thien-Tanner (PTT) laminar
visco-elastic model is also similar to the Maxwell model but
includes an additional “extensibility” term in the equation for
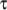 ,
suitable for polymeric liquids:
,
suitable for polymeric liquids:
![∂τ νM 1 ( 𝜀λ ) ---+ ∇ ∙(Uτ) = 2symm [τ∙∇U ]− 2---symm (∇U )− -exp − ---tr(τ) τ ∂t λ λ νM \relax \special {t4ht=](img/index585x.png) |
(7.29) |
 (epsilon) is the
extensibility parameter. An example specification of model
parameters is shown below:
(epsilon) is the
extensibility parameter. An example specification of model
parameters is shown below:
simulationType laminar;
laminar
{
model PTT;
PTTCoeffs
{
nuM 0.002;
lambda 0.03;
epsilon 0.25;
}
}
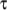 is a sum of
stresses, each with an associated relaxation time
is a sum of
stresses, each with an associated relaxation time 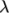 and extensibility
coefficient
and extensibility
coefficient  .
.
7.3.10 Lambda thixotropic model
The Lambda
Thixotropic laminar model calculates the
evolution of a structural parameter 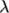 (lambda) according to:
(lambda) according to:
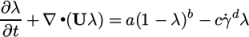 |
(7.30) |
 ,
,  ,
,  and
and 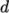 . The viscosity
. The viscosity  is then calculated
according to:
is then calculated
according to:
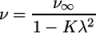 |
(7.31) |
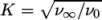 . The viscosities
. The viscosities  and
and  are limiting values
corresponding to
are limiting values
corresponding to 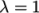 and
and 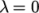 .
.
An example specification of the model in momentumTransport is:
simulationType laminar;
laminar
{
model lambdaThixotropic;
lambdaThixotropicCoeffs
{
a 1;
b 2;
c 1e-3;
d 3;
nu0 0.1;
nuInf 1e-4;
}
}

