OpenFOAM v11 User Guide - 5.1 Mesh description

5.1 Mesh description

This section provides a specification of the way OpenFOAM describes a mesh. The mesh is an integral part of the numerical solution and must satisfy certain criteria to ensure a valid, and hence accurate, solution. OpenFOAM defines a mesh of arbitrary polyhedral cells in 3-D, bounded by arbitrary polygonal faces, i.e. the cells can have an unlimited number of faces where, for each face, there is no limit on the number of edges nor any restriction on its alignment. This flexible description of a mesh offers great freedom in mesh generation and manipulation when the geometry of the domain is complex.

An OpenFOAM mesh begins with points (or vertices). Each point is a location in 3D space, defined by a vector. The set of points forms a list where each point can be indexed by its position in the list, starting from zero. The list does not contain points that are unused.

The points are used to from mesh faces, where each face is defined as an ordered list of points, described by their where a point is referred to by its label. The ordering of point labels in a face is such that each two neighbouring points are connected by an edge, i.e. you follow points as you travel around the circumference of the face. The set of faces forms a list where each face is referred to by its label, representing its position in the list.

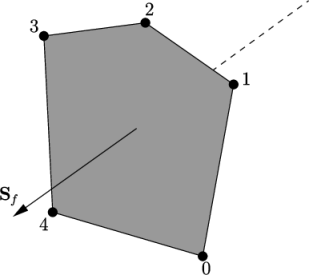
Each face can be characterised by a vector whose direction is normal to the face. The normal vector follows the right-hand rule, i.e. looking towards a face, if the numbering of the points follows a clockwise path, the normal vector points away from you, as shown in Figure 5.1 . Note that faces can be warped, i.e. the points of the face may not necessarily lie on a plane.

There are two types of face, described below.

• Internal faces, which connect two cells (and it can never be more than two). For each internal face, the ordering of the point labels is such that the face normal points into the cell with the larger label, i.e. for cells labelled ‘2’ and ‘5’, the normal points into ‘5’.
• Boundary faces, which belong to one cell since they coincide with the boundary of the domain. A boundary face is therefore addressed by one cell(only) and a boundary patch. The ordering of the point labels is such that the face normal points outside of the computational domain.

A cell is a list of faces in arbitrary order. Under normal circumstances, cells must have the properties listed below.

• The cells must be contiguous,i.e. completely cover the computational domain and must not overlap one another.
• Every cell must be closed geometrically, such that when all face area vectors are oriented to point outwards of the cell, their sum should equal the zero vector to machine accuracy;
• Every cell must be closed topologically such that all the edges in a cell are used by exactly two faces of the cell in question.

The boundary is formed by the boundary faces. It should be closed, i.e. the sum all boundary face area vectors equates to zero to machine tolerance. It is split into regions known as patches so that different boundary conditions can be applied to different parts of the boundary. A patch is defined by the labels of the faces it contains.